有限仿射空间(finite affine)是一类组合构形，它由q阶n维射影空间PG(n，q)中去掉一个超平面而得到，记为EG(n，q)。1

基本介绍有限仿射空间EG(n，q)中一条线上含q个点，共有qn个点，任一k维子空间含qk个点，以EG(n，q)中的全部k维子空间作为区组，可以得到一个(qn，qk，λ)-BIBD，其中1

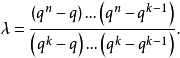
相关介绍仿射空间

定义1 V是数域F上的向量空间，A是一个非空集合，称A是V上的仿射空间，如果有一个从A×V到A的映射：(p，α)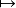 p+α具有以下性质：

(1)对任意p∈A及V中的零向量0，p+0=p；

(2)对任意p，q∈A，存在唯一的向量α∈V，使得p+α=q；

(3)对任意p∈A，α，β∈V，p+(α+β)=(p+α)+β．

V上的仿射空间A也记作A(V)，其元素称为点。

将A(V)的维数定义为向量空问V的维数，即dim A(V)一dim V，0维、1维、2维的仿射空间分别称为点、仿射直线、仿射平面，比如A(E2)就是一个仿射平面。

对A中的任意两点p，q，都存在唯一向量α，使得p+α=q。记α为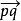，称p和q为α的起点和终点，因为p+0=p，所以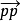=0。另外，对A中的任意三点p，q，r，

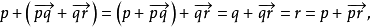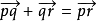所以，令r=p，得。

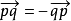例 1 数域F上的向量空间V也可以看成是自身上的一个仿射空间。此时，非空集合A就是V本身，V中的向量同时也看成点，点与向量的加法就定义为向量间的加法，它自然会满足(1)-(3)。所以，每个向量空间同时也可视为一个仿射空间。特别地，Fn可视为向量空间Fn上的一个仿射空间。

定义2 A是向量空间V上的n维仿射空间，A中的一个点0和V的一个基ε₁，ε₂，…，εn称为A的一个仿射坐标系，记为[o；ε₁，ε₂，…，εn]，点o称为原点，向量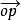在这个基下的坐标称为点P的仿射坐标2。

有限射影空间

有限射影空间是一类组合构形，满足以下公理的有限点集上的关联系统：1.对两相异点，有且仅有一条线含这两个点；2.若A，B，C是不共线的三点，D是含A，B的线上异于A的点，E是含A，C的线上异于A的点，则含D，E的线与含B，C的线含一个公共点F；3.每条线至少含三个相异点。

若射影空间的某个子集在含一条线上的两个点时必含这条线上所有的点，则称该子集为子空间.将点称为零维子空间，线称为1维子空间，由此可归纳地定义子空间的维数.若子空间Xn-1的维数为n-1，P是射影空间中不属于Xn-1的一点，将含P及Xn-1中任一点的所有线上的点的全体记为Xn，则Xn是子空间，其维数定义为n.在n维射影空间中，2维子空间称为平面，n-1维子空间称为超平面.若某条线上含q+1个点，则每条线上都含q+1个点，此时称射影空间是q阶的.q阶n维射影空间记为PG(n，q).将q元有限域上n+1维向量空间中的一维子空间取作“点”，2维子空间取作“线”，便得到n维射影空间PG(n，q)的一个例子.这样的“点”可用一个n+1维的非零向量(x1，x2，…，xn+1)表示，当λ为有限域中非零元时，向量λ(x1，x2，…，xn+1)将表示同一个“点”.称(x1，x2，…，xn+1)为射影空间中点的齐次坐标.PG(n，q)中共有

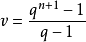个点，一个超平面含k=(qn-1)/(q-1)个点，若将一个PG(n，q)中所有超平面取作区组，则得到一个(v，k，λ)-BIBD，其中

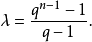当n≥3时，PG(n，q)在同构的意义下是惟一的，但是，当n=2时，存在不同类型的射影平面1。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学