格隆斯基不等式是格隆斯基(Grunsky,H.)于1939年给出的一个不等式，它是面积原理的一种推广，是研究单叶函数的重要手段之一。

定义格隆斯基不等式是格隆斯基(Grunsky,H.)于1939年给出的一个不等式，它是面积原理的一种推广，是研究单叶函数的重要手段之一。1

具体表述格隆斯基不等式的具体表述如下：

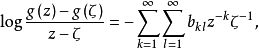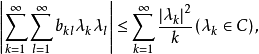设g∈∑， 则 这里∑表示单位圆外的一类单叶函数，即∑类。

面积原理面积原理亦称格朗沃尔面积定理，是∑类函数展开式系数的一个性质定理。此定理由格朗沃尔(Gronwall , T. H.)于1915年提出。

该定理断言：若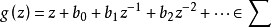，则。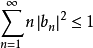

之所以称其为面积原理，是因为定理的结论是根据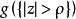的余集的面积大于零的几何事实而得到的，这里ρ可以是任何大于1的数。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学