广义最大模定理是最大模定理的推广。最大模定理是复变函数论中有关函数值的模的一个重要而有用的定理，断言解析函数的模在区域内部不能达到极大值，除非它是常数函数。

定义广义最大模定理是最大模定理的推广。

设f(z)在有界区域D内解析且有界，若在D的边界上除去有限个点ξ1,ξ2,...,ξn外，有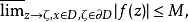则在D内恒有|f(z)|≤M。1

最大模定理最大模定理是复变函数论中有关函数值的模的一个重要而有用的定理，断言解析函数的模在区域内部不能达到极大值，除非它是常数函数。

这一原理可具体表述如下：设ƒ(z)为有界域G内全纯并在闭域G并上其边界上连续的函数，以M(дG,ƒ)表示|ƒ(z)|在G的边界дG上的最大值，则在G内恒有|ƒ(z)|