多面体拟阵(polymatroid)是一类整多面体,是与拟阵多面体有关的一个概念,可分为有界多面体拟阵和无界多面体拟阵。
基本介绍设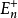 为n维欧氏空间的那个非负象限,在
为n维欧氏空间的那个非负象限,在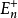 上定义一个偏序:对于
上定义一个偏序:对于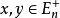 ,
,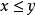 表示
表示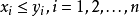 ,设
,设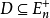 ,若
,若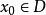 具有这样的性质:不存在
具有这样的性质:不存在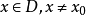 ,使得
,使得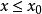 ,则称x0为偏序D上的一个极小元,若不存在
,则称x0为偏序D上的一个极小元,若不存在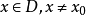 ,使得
,使得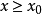 ,则x0为D上的一个极大元,在
,则x0为D上的一个极大元,在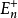 上的一个有界多面体拟阵就是这样的一个多面体M,它具有性质:
上的一个有界多面体拟阵就是这样的一个多面体M,它具有性质:
1.若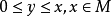 ,则
,则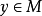 ;
;
2.对任何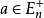 ,集合
,集合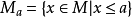 的所有极大元的分量和均相同,并且,这个和称为a的秩。
的所有极大元的分量和均相同,并且,这个和称为a的秩。
在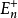 上所定义的秩确定一个多面体拟阵的秩函数,在
上所定义的秩确定一个多面体拟阵的秩函数,在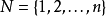 的所有子集形成的簇2N上定义的函数ρ,若对任何
的所有子集形成的簇2N上定义的函数ρ,若对任何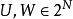 均有
均有
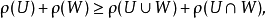 则称ρ为次模的,若上面的不等式是反向的,则称ρ为上模的1。
则称ρ为次模的,若上面的不等式是反向的,则称ρ为上模的1。
有界多面体拟阵一个多面体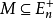 是有界多面体拟阵,当且仅当在2N上存在一个非降的次模函数
是有界多面体拟阵,当且仅当在2N上存在一个非降的次模函数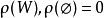 ,使得
,使得
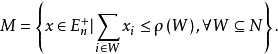
无界多面体拟阵在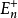 上的一个无界多面体拟阵就是这样的一个多面形Q,使它具有性质:若
上的一个无界多面体拟阵就是这样的一个多面形Q,使它具有性质:若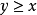 ,和
,和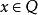 ,则
,则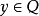 ;对任何
;对任何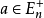 ,在
,在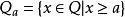 中的每个极小元的分量和都相同,一个多面形
中的每个极小元的分量和都相同,一个多面形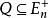 是一个无界多面体拟阵,当且仅当存在2N上的一个上模函数
是一个无界多面体拟阵,当且仅当存在2N上的一个上模函数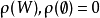 ,使得1
,使得1
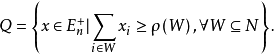
多面体拟阵的序阵多面体拟阵的序阵(polymatroid greedoid)是一种组合构形,它是由多面体拟阵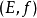 派生的序阵
派生的序阵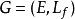 ,这里f为符合要求的次模函数,序串
,这里f为符合要求的次模函数,序串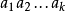 为序阵G的可行词,当且仅当对于任意的
为序阵G的可行词,当且仅当对于任意的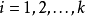 ,均有
,均有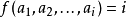 。例如,在偏序集
。例如,在偏序集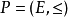 上,对于E的任意子集X,设
上,对于E的任意子集X,设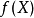 表示由X产生的理想
表示由X产生的理想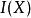 包含元素的个数,此时
包含元素的个数,此时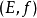 为一多面体拟阵,于是,可由
为一多面体拟阵,于是,可由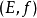 派生序阵,记为
派生序阵,记为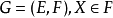 当且仅当X为P上的一个理想,称
当且仅当X为P上的一个理想,称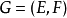 为偏序集序阵,或时间表序阵1。
为偏序集序阵,或时间表序阵1。
相关介绍拟阵多面体是一种组合构形,它是由拟阵M=(E,I)的所有独立集的关联向量生成的多面体P。
记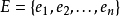 ,独立集I的关联向量
,独立集I的关联向量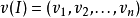 ,当I包含元素ei时,vi=1,否则vi=0,拟阵多面体的优越性在于,它可以借助拟阵的秩函数r而表示为约束不等式的形式I(E,r):对于E的任意子集F,有
,当I包含元素ei时,vi=1,否则vi=0,拟阵多面体的优越性在于,它可以借助拟阵的秩函数r而表示为约束不等式的形式I(E,r):对于E的任意子集F,有
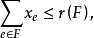 且对于E的任意元素e,有
且对于E的任意元素e,有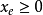 ,拟阵多面体P的顶点均为整值点,这样建立在拟阵上的优化问题就可以归结为不考虑其解是否取整数值的一般线性规划问题,从而为拟阵上的优化问题开辟了一个新的领域,例如,下图G上的图拟阵M(G),其多面体由下述不等式决定1:
,拟阵多面体P的顶点均为整值点,这样建立在拟阵上的优化问题就可以归结为不考虑其解是否取整数值的一般线性规划问题,从而为拟阵上的优化问题开辟了一个新的领域,例如,下图G上的图拟阵M(G),其多面体由下述不等式决定1:
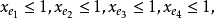
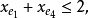
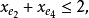
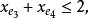
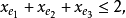
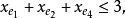
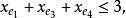
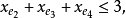
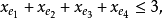
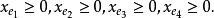
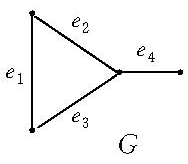
在以约束不等式表示的拟阵多面体里,若以G的满足下述条件的一般整值次模函数f取代拟阵的秩函数:
1.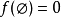 ;
;
2.对于E的任意子集A,B,若A⊆B则:
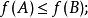
3.对于E的任意子集A和B,有
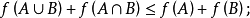 则不等式组I(E,f)决定的多面体,其顶点仍对应于某个拟阵的独立集,由I(E,f)决定的拟阵称为多面体拟阵1。
则不等式组I(E,f)决定的多面体,其顶点仍对应于某个拟阵的独立集,由I(E,f)决定的拟阵称为多面体拟阵1。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

