Havel-Hakimi算法是图论中解决图形实现问题的算法。 也就是说，它回答了以下问题：给定一个非负整数的有限列表，是否有一个简单的图形，使得它的度序列恰好是这个列表。 这里，“度序列”是一个数字列表，对于图的每个顶点，它表示它有多少个邻居。 对于肯定答案，整数列表称为图形。 该算法构造一个特殊的解决方案，如果存在或证明一个人找不到肯定的答案。 这种结构基于递归算法。 该算法由Havel（1955）出版，后来由Hakimi（1962）出版。

介绍1，Havel-Hakimi定理主要用来判定一个给定的序列是否是可图的。

2，首先介绍一下度序列：若把图 G 所有顶点的度数排成一个序列 S，则称 S 为图 G 的度序列。

3，一个非负整数组成的有限序列如果是某个无向图的序列，则称该序列是可图的。

4，判定过程：（1）对当前数列排序，使其呈递减，（2）从S[2]开始对其后S[1]个数字-1，（3）一直循环直到当前序列出现负数（即不是可图的情况）或者当前序列全为0 （可图）时退出。

5，举例：序列S：7,7,4,3,3,3,2,1 删除序列S的首项 7 ，对其后的7项每项减1，得到：6,3,2,2,2,1,0，继续删除序列的首项6，对其后的6项每项减1，得到：2,1,1,1,0，-1，到这一步出现了负数，因此该序列是不可图的。

算法Havel–Hakimi算法基于以下定理1。

令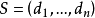 为有限多个非负整数组成的非递增序列。 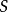可简单图化当且仅当有穷序列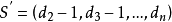只含有非负整数且是可简单图化的。

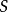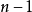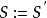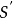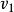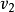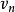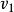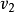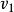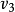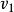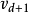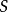如果给定的序列是可简单图化的，那么算法最多运行次赋值。注意每次赋值后可能需要重新对序列排序。当全部为零时，算法停止。在每一步中，如果序列可简单图化，就从向,各引出一条边，即{,},{,},{,}，然后令约化为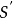。如果在任何一步中，序列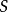无法约化为非负整数序列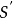，算法就给出最开始的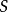不可简单图化的结论。

代码#include #include #include using namespace std; struct node { int num,e; }x[15]; bool map[15][15]; int cmp(node a,node b) { if(a.num==b.num) return a.eb.num; } int judge(int n) { int i,num,tmp; while(1){ sort(x+1,x+n+1,cmp); if(!x[1].num) return 1;//数组全为 0 的情况退出 for(i=2;i0){ x[i].num--; map[x[1].e][x[i].e]=map[x[i].e][x[1].e]=1; } else return 0; } x[1].num=0; } } int main() { int n,t,i,j; bool flag; scanf("%d",&t); while(t--){ scanf("%d",&n); for(i=1;i