弱∗列紧是与弱∗收敛相联系的列紧性。弱（弱∗）列紧以及弱（弱∗）收敛、弱（弱∗）序列完备等都是赋范线性空间理论中的重要概念。

简介弱∗列紧是与弱∗收敛相联系的列紧性。弱（弱∗）列紧以及弱（弱∗）收敛、弱（弱∗）序列完备等都是赋范线性空间理论中的重要概念。

设X是赋范线性空间，S是共轭空间X*的子集。如果S中任何点列{fn}都有弱∗收敛的子序列，则称S是弱∗列紧的。

当X可分时，X*中点集的有界性与弱∗列紧性等价。1

弱∗收敛弱∗收敛是一种收敛性，指依弱∗拓扑收敛。

设X*为局部凸空间X的共轭空间，定向列{fα}⊂X*弱∗收敛于f∈X*，记为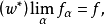其充分必要条件是对任意的x∈X都有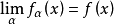成立。

赋范线性空间赋范线性空间(normed linear space)是在线性空间中引进一种与代数运算相联系的度量，即由向量范数诱导出的度量。赋范线性空间称为Banach空间，是指由范数导出的度量是完备的。

定义：设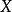是线性空间，函数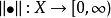称为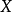上定义的一个范数，如果满足：

（1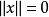）当且仅当；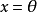

（2）对任何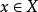及，；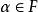

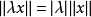（3）对任意，。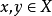

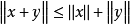称二元体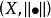为赋范线性空间。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学