李普希茨连续映射是满足所谓李普希茨条件的连续映射。李普希茨连续映射必是一致连续映射。

简介李普希茨连续映射是满足所谓李普希茨条件的连续映射。

设有映射f:D⊂X→Y。若有正常数L，使得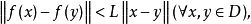则称f:D→Y为李普希茨连续映射。其中正常数L称为李普希茨常数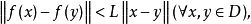，称为李普希茨条件。

性质李普希茨连续映射必是一致连续映射。1

连续映射(continuous mapping)

连续映射是拓扑空间之间的一类重要映射。

设(X,T)与(Y,Τ)是两个拓扑空间，f:X→Y是映射，x∈X。若f(x)的每一邻域关于f的原像是x的邻域，则称f在点x处是连续的。若f在X的任意点是连续的，则称f是(X,T)到(Y,U)的连续映射。

一致连续映射(uniformly continuous mapping)

一致连续映射是一致空间上的一类重要映射。设(X，U)，(Y，V)是两个一致空间，f：X→Y。若对于任意V∈V，存在U∈U使得当(x，y)∈U时有(f(x)，f(y))∈V，则称f关于U和V是一致连续的，简称f是一致连续映射。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院