若f在x0加托可微，且Df(x0;h)关于h∈X是线性的，则称f在x0有线性弱微分，此时存在线性算子A:X→Y，使得Df(x0;h)=Ah(∀h∈X)，这个线性算子称为f在x0的加托导算子。

简介设X和Y是赋范线性空间，Ω是X中的开集，f:Ω→Y是映射，x0∈Ω。

若f在x0加托可微，且Df(x0;h)关于h∈X是线性的，则称f在x0有线性弱微分，此时存在线性算子A:X→Y，使得Df(x0;h)=Ah(∀h∈X)，这个线性算子A常记为Df(x0)（或df(x0)，或f'(x0)），称为f在x0的加托导算子（简称G导算子）或弱导算子。

性质如果加托导算子Df(x0)还是有界的，则称f在x0有有界线性弱微分。

习惯上，当谈到f在x0加托可微时，常指f在x0有有界加托导算子的情形。1

加托可微设X和Y是赋范线性空间，Ω是X中的开集，f:Ω→Y是映射，x0∈Ω。设h∈X，若极限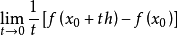存在，则该极限值称为映射f在点x0沿方向h的加托微分（或G微分）或弱微分，记为Df(x0;h)。

若f在x0沿任何方向h的弱微分均存在，则称f在点x0加托可微（或G可微）或弱可微。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院