迹正线性泛函是C*代数上一类具有类似于矩阵迹性质的正线性泛函。当φ(a*a)=0蕴涵a=0时，称φ是忠实的迹正线性泛函。

简介迹正线性泛函是C*代数上一类具有类似于矩阵迹性质的正线性泛函。

设φ是C*代数?上正线性泛函，如果对任意a∈?都有φ(a*a)=φ(aa*)成立（或等价地，对任意b,c∈?都有φ(bc)= φ(cb)成立），则称φ是迹正线性泛函或φ是迹的。

推广进而，当φ(a*a)=0蕴涵a=0时，称φ是忠实的迹正线性泛函。

这个概念也可推广到正线性映射的情形。1

正线性泛函（positive linear functional）

正线性泛函是在正元上取非负值的线性泛函。

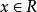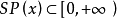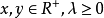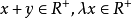设 R 是有单位元e的C*代数，，如果x=x*且，则称x为 R 中的正元。正元的全体记为 R+。当时，有，而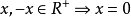，因此，R+是 R 中的锥，R+ 是闭集，设f是R上的线性泛函。

如果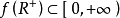，则称 f 是 R 上的正线性泛函，正线性泛函必是有界的，且

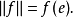
本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院