埃尔米特-费耶尔插值多项式（Hermite-Fejer interpolation polynomials）是埃尔米特插值的一种特殊情况。

简介

埃尔米特-费耶尔插值多项式是埃尔米特插值的一种特殊情况。

设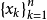 是[-1,1]上的一组互异的点，记 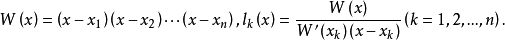对于f∈C[-1,1]，称 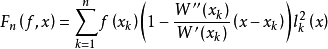为函数f(x)的以 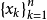为结点组的埃尔米特-费耶尔插值多项式。

逼近

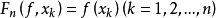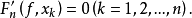Fn(f,x)是一个2n-1次代数多项式，它满足如下条件： 及 20世纪70年代以来，人们对Fn(f)逼近f的研究甚多，常称用Fn(f)对f的逼近为埃尔米特-费耶尔插值多项式逼近。1

埃尔米特插值

不少实际的插值问题不但要求在节点上的函数值相等，而且还要求对应的导数值也相等,甚至要求高阶导数也相等，满足这种要求的插值多项式就是埃尔米特插值多项式。

埃尔米特插值是另一类插值问题，这类插值在给定的节点处，不但要求插值多项式的函数值与原函数值相同。同时还要求在节点处，插值多项式的一阶直至指定阶的导数值，也与被插函数的相应阶导数值相等，这样的插值称为埃尔米特(Hermite)插值。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学