作为逼近集G，取作X的凸集，则称为凸逼近。例如实变函数逼近中的共单调逼近等都是凸逼近。

简介逼近集设X是距离空间，其元素（或者称为点）x与y之间的距离记为ρ(x,y)。设G是X的一个子集，称

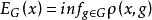为x与G之间的距离，它自然标志着G对x的逼近程度，常称它为G对x的最佳逼近值，又称G为逼近集。

倘若G中有元素g0使得ρ(x,g0)=EG(x)，则称g0为x在G中的最佳逼近元。

定义作为逼近集G，取作X的凸集，则称为凸逼近。

例如实变函数逼近中的共单调逼近等都是凸逼近。1

凸集令S是实数上的向量空间，或者更一般地，是在某个有序域上，这包括欧几里德空间。如果对于C中的所有x和y，并且在区间(0,1)中的所有t，点(1-t)x+ty也属于C，则S中的集合C被称为凸。

换句话说，连接x和y的线段上的每个点都在C中。这意味着实际或复杂拓扑向量空间中的凸集是路径连接的。此外，如果除了端点之外的连接x和y的线段上的每个点都在C的内部，则C是严格凸起的。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学