常高斯曲率的曲面基本介绍
常高斯曲率的曲面(surfaces with constant Gauss curvature)是一类重要的曲面,它是高斯曲率K为常数的曲面。在曲面上选择适当的参数系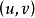 ,可以使:
,可以使:
当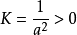 时,
时,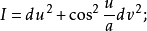
当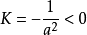 时,
时,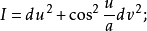
当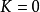 时,
时,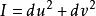 。
。
因为有相同常高斯曲率的曲面在局部上总是等距等价的,所以,K=0的曲面在局部上都与平面等距等价的;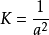 的曲面在局部上都与半径为a的球面等距等价;
的曲面在局部上都与半径为a的球面等距等价;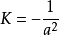 的曲面在局部上都与伪球面等距等价1。
的曲面在局部上都与伪球面等距等价1。
伪球面重物置于一直道之外,人用绳拖此重物并沿直道向前走时重物所经过的轨迹线叫曳物线。将此曳物线绕直道为轴旋转一周后所形成的曲面称为“伪球面”。罗巴切夫斯基等所发现的非欧几何学可以在某种意义下在伪球面上实现2。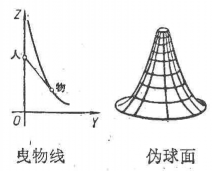
伪球面(pseudo-sphere)是一类重要的曲面,它是高斯曲率为负常数的曲面,它是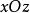 平面上的曳物线
平面上的曳物线
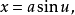
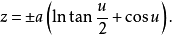 绕z轴旋转而成的曲面:
绕z轴旋转而成的曲面:
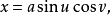
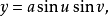
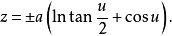 它在u=0的点处是不光滑的,因而是非正则的。在正则点,其高斯曲率为
它在u=0的点处是不光滑的,因而是非正则的。在正则点,其高斯曲率为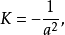 它可以作为罗氏几何的一个模型1。
它可以作为罗氏几何的一个模型1。
常平均曲率曲面常平均曲率曲面(surfaces with constant mean curvature)是一类重要的曲面,它是平均曲率H为常数的曲面。例如,球面是常平均曲率曲面,此外,将一椭圆在其平面内一条定直线l上滚动,其焦点所画出的平面曲面C绕直线l旋转所生成的旋转曲面也是常平均曲率曲面。上述命题称为德洛内定理,若曲线C的曲率半径为R,C的法线被曲线C与定直线所截的长为N,则有关系式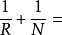 常数1。
常数1。
来源: 百度百科


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

