芝诺的乌龟

芝诺是古希腊的哲学家，数学家。芝诺的乌龟（二分法悖论）是芝诺提出的四个悖论（芝诺悖论）中的第一个悖论。这四个悖论都是用来维护巴门尼德的存在学说：

存在学说：认为存在是永恒的，是太一，连续不可分；存在是不动的，是真实的，可以被思想。感性世界的具体事物是非存在，是假相，不能被思想。

换句话说，巴门尼德的存在论认为，存在是唯一真实的事物，而变化、运动、时间和空间等现象都是虚幻的。他认为，存在不可能从无到有地产生，也不可能从有到无地消失，存在是永恒、不可分割、不可变化的。因此，我们所看到的一切都是存在的不同形式和表象，而不是真正的实体。

在了解了巴门尼德的存在论，我们先来看这样一个问题：

现在我们想要从A点走到B点，那么中途就一定会经过C点。而从C点走到B点又一定会经过D点（假设C为AB中点，D为CB中点，以此类推）那么我们就会经过无穷多个中间点，因此这个过程也会一直循环下去，这样我们将永远无法到达B点。

关于这个悖论，最常见解法是：

假设从A到B点需要的时间为1，那么从A到C点所需的时间就是1/2。以此类推，所以我们就可以获得一个等比数列：

S = 1/2+1/4+1/8+1/16+...

而形如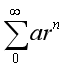的级数，如果满足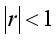，则级数收敛。因此级数S一定会收敛于一个有限值M，所以从A到B需要的时间有限。

而芝诺的乌龟描述的是，假设我们从原点开始追距离我们10米处的乌龟，那么每当我们要追到乌龟时，乌龟都会向前移动一小段距离，当我们再次前几到乌龟移动的位置时，乌龟在我们移动的这一小段时间内又向前爬行了一段距离，以此类推。芝诺据此诡辩道，因为我们要追赶无穷多段距离，不论我们跑的有多快，永远也无法追上爬的很慢的乌龟。

但实际上，芝诺的那个时代所不清楚的是，无穷多段距离的和可以是有限的，追赶无穷多段距离的时间之和也可以是有限的。

接下来我们来用数学推导说明一下芝诺诡辩的核心所在：

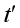这个悖论的本质是两种不同度量的比较，一个是普通钟，在这个普通钟里，我们最终可以追上乌龟，而另一个就是“芝诺钟”,在芝诺钟里，我们将永远无法追上乌龟。

开始时假设我们与乌龟相距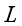，我们与乌龟的速度分别为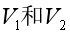，那么我们显然有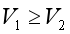。所以在普通钟里，我们追上乌龟所需的时间为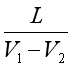。而对于芝诺钟，假设其初始值为0，每当我们达到乌龟本来所在的位置时，其数值+1。（注意到，在假象的“芝诺时间”里，不管每次追赶距离是否越来越小，经历的“时间”始终为1，保持不变。）比赛过程如下：

1. 比赛开始时，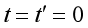

2. 我们第一次达到乌龟所在的位置，，。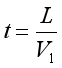

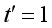3. 我们第二次达到乌龟所在的位置，，。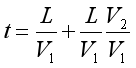

...以此类推...

4.,。

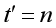因此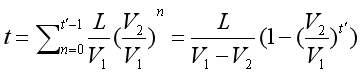

可知。画图可知（假设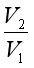为0.5）

因此当时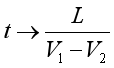，。所以从芝诺钟的角度来看，我们永远也无法追上乌龟。这里，芝诺把经过无穷多段距离所需要的时间都看成“1”，并没有考虑到距离的不同所用的时间也不同，这才有了这一悖论。

关于这个问题，网络上也有一个很有趣的回答，虽然只有一句话，但是却能抓住这个悖论的关键：芝诺的乌龟这个悖论可以理解为，我们在追上乌龟之前，永远没办法追上乌龟！

来源: 原创