微积分？听起来很高大上！我也能懂吗？

作者郑重承诺：读懂这篇科普最多需要初中数学知识！而且大部分不需要数学知识，只需要观察力和想象力！

微积分是高等数学的重要组成部分。它表现了运动和变化的思想，让数学从静态走向动态。上至三体问题，下至投篮抛物，要想精确求解，都离不开微积分这一工具。

微积分主要包含三大部分：极限论、微分学、积分学（这会儿知道为什么叫“微积分”了吧？）。

这次微积分科普，会围绕我们的老朋友进行：圆周率π。

没错！就是圆的周长与直径的比，是一个无限不循环小数：3.1415926……

今年是中国古代数学家刘徽诞辰1800周年。刘徽为了得出准确的圆周率，创造了一种名叫“割圆术”的算法。所谓“割圆”，就是画圆内接正多边形，增加边数。他说：“割之弥细，所失弥少。割之又割，以至于不可割，则与圆周合体而无所失矣。”

这里有一个重要概念：无限。一个重要方法：逼近。

看这张图，随着边数增加，多边形越来越接近圆，其周长也越来越接近圆的周长。

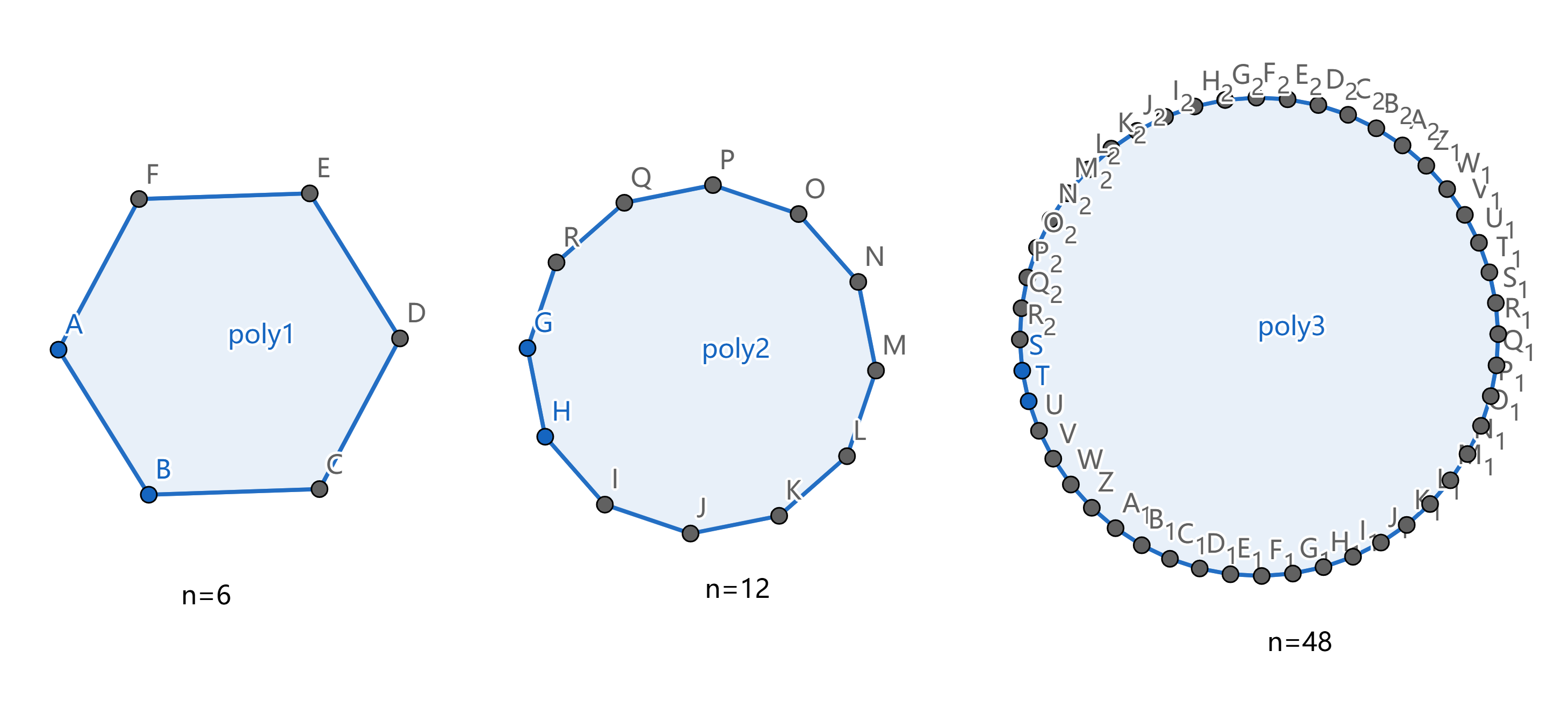
为了思考无限，我们用越来越大的数字来逼近它。48条边的正多边形，虽然不是“无限”条边，但也很接近圆了吧？所以我们稍微想象一下，就可以猜到：有无限条边时，多边形就变成了圆！

上面的过程体现了“极限思想”。所谓极限，就是“趋势”。我们把直径为1的正六边形的周长记做C6，正12边形周长是C12……以此类推。

看这一串数：C6=3，C12≈3.096……Cn。当n越来越大的时候，Cn就越来越接近π。

换句话说，当n大到一定程度的时候（比如n=48），Cn与π的“距离”非常小。数学上用两个数的差的绝对值，来描述它们的距离。

再精细一些，把上面的“一定程度”换成某个大数N，“非常小的距离”换成任意的正数。当边数n大于N时，Cn-π的绝对值（距离）小于一个任意小的正数ε（N越大ε越小）。这时把π称为数列Cn的极限，称“Cn趋于π”。

这就是数列极限的定义。

让我们回到用割圆术求π，思路是这样的：

求π只需求出圆的周长，再除以直径。首先是把正n边形的边长累加，然后，让n一直增大。当n趋于无穷大，累计周长就趋于π了。

所以我们不急于让n变大。先固定n，得出累加表达式，再求极限！

看这张图（以n=6为例），我们把圆画在一个坐标系里，圆心就是原点。把正n边形边长写作ds（前面加d表示“非常小”），边长的水平距离是dx，垂直距离是dy。

现在要用到初中的“勾股定理”：

ds2=dx2+dy2.

但同时知道dx、dy有点麻烦，可以换一种写法，只保留dx吗？

我们现在处理的是直线，初中数学有“斜率”k的概念。在这里，k=dy/dx。所以dy=k•dx.

换一种写法:

ds2=dx2+k2dx2=(1+k2)dx2.

那么，正n边形的周长就是：

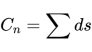
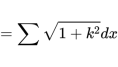
等号右边的怪符号表示求和。

因为在多边形不同的边上，k是不一样的。当n越来越大时，ds越来越短，dx也越来越短，多边形上每一点就对应一个斜率k。当我们用dx代替n来表示周长Cn，这个式子就是以多边形上一点的横坐标x为自变量的函数。

函数极限的定义与数列极限类似：当Cn与π的距离小于任意正数ε（非常近），如果有正数δ，dx与0的距离小于δ。这时就叫dx趋于0时，Cn趋于π。

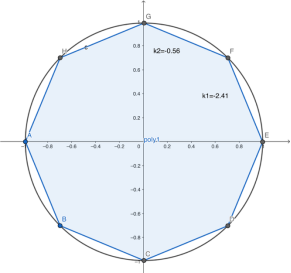
当n趋于无穷大（dx趋于0）时，正多边形不复存在，k的几何意义是什么呢？

我们以任意一条边为例观察：边与圆有两个交点，这种线叫做圆的“割线”。我们固定其中一点，当n增大，割线与圆的两个交点越来越近，最终会是什么呢？

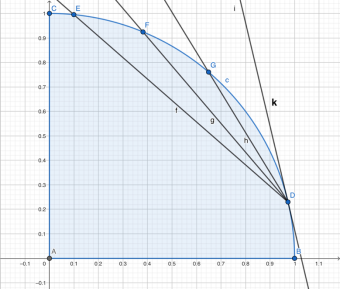
两个交点合而为一！割线变成了切线！

所以，当n趋于无穷大，k的几何意义就是该点切线的斜率！

在微积分中，我们把k叫做“导数”，如图所示的k就是函数y=f(x)在点D处的导数。

导数可表示为

f(x)'=dy/dx.

导数是微分学的核心。

如果把上式换个写法：

dy=f(x)'dx.

又是什么意思呢？

dx是一段非常小的横向距离（x的变化量），乘上x的导数之后，就是对应的纵向距离。如果知道了函数f(x)，而且点(x，f(x))存在导数，就可以根据求导法则求出f(x)在该点的导数，借此得到dy。当dx非常小的时候，dy非常接近于y的变化量。也就是说，可以用直线估计曲线！在微积分角度看，只有把dx取得足够小，曲线的微观部分就是直线！

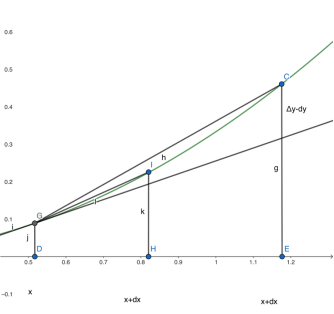
由图片可知，当dx越来越接近0，y的变化量Δy和dy的差就越来越小，最终可以用dy估计Δy的变化量（曲线也越来越接近直线）。

这时，我们把dy叫做“微分”。

需要指出，导数和微分存在的前提是函数连续。借助图像来说，如果圆有缺口，缺口处就没有切线！因此该点没有导数和微分！

反过来，如函数可导，则函数连续。

现在回到求圆周率，我们要算的是n趋于无穷大时累计和的极限。

把累计和表示为：

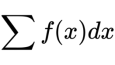
其中x的大小在两个实数a、b之间。

如果函数f(x)是连续的，那么dx趋于0时，累计和的极限叫做“定积分”。a叫积分下限，b叫积分上限。写作：

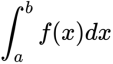
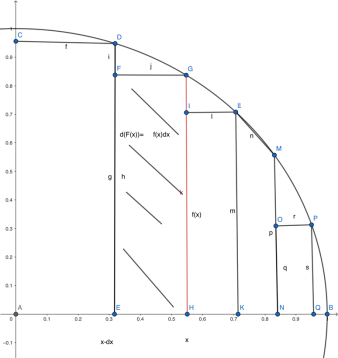
我们知道dx是横向的一小段，而对每一个dx，f(x)是对应的函数值，所以f(x)dx就是一个窄矩形的面积（如图）。对这一系列矩形求和，取极限（dx趋于0），就是函数f(x)下曲边梯形的面积（由函数图像、x轴、纵向直线x=a和x=b围成）！这就是积分的几何意义。

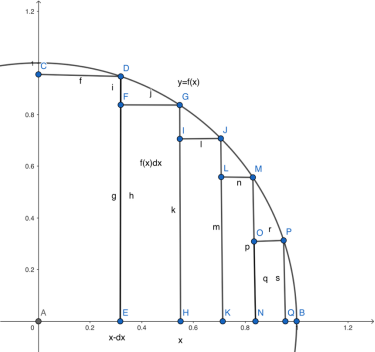
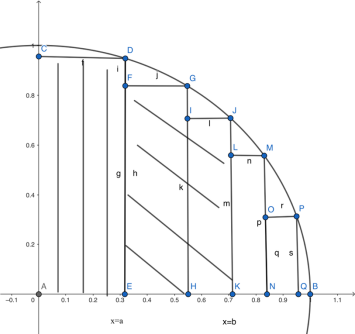
斜线阴影部分即x=a、x=b之间的曲边梯形

但是我们刚才只掌握了微分学，如何把求面积跟微分学建立联系呢？微分是“化整为零”从而“化曲为直”，而积分是“化整为零”之后“集腋成裘”，二者好像很难关联起来。

数学有一个重要思维叫“化归”，也就是重新表达问题，使之变成已经解决的问题。我们现在需要造出一座桥梁，把积分和微分打通！

接下来介绍一个重磅公式：牛顿-莱布尼茨公式。

我们提出一个新函数，叫“原函数”：

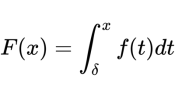
其中，t是自变量（δ≤t≤ε），函数f(t)在这一区域存在积分，x也在这一区域中。

根据定积分的几何意义，原函数就是f(t)、水平轴、直线t=δ和t=x围成的曲边梯形的面积。

由上图可得，我们要求的面积，是自δ到b的面积减去δ到a的面积（阴影部分减竖线阴影部分，就是斜线阴影部分），所以用数学语言表达：

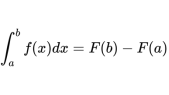
那么，只要把原函数F(x)和微分学建立联系，问题就解决了！

现在思考一个问题：对F(x)求导数（自变量为x），会得到什么？

我们已经知道，函数f(x)的导数可表示为dy/dx。dx趋于0时，dy是函数变化量。

根据定积分的几何性质，可以知道原函数的变化量是一个很窄的曲边梯形，面积就是f(x)dx。现在把它再“除”dx，得到的就是f(x)！所以，对一个函数求原函数后，再求导数，会得到最初的函数！换句话说，求原函数是求导的逆运算（就像加法是减法的逆运算）。积分和微分成功建立了联系！

因此，F(x)’=f(x)。

如果几个函数只相差一个任意常数，对它们求导的结果是一样的（平移曲线不会改变形状，所以各点斜率不变）。用C表示常数，则

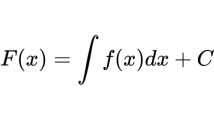
我们把新式子中的

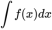
称为不定积分。根据求原函数与求导之间是逆运算的关系，给出不定积分表。可以通过不定积分表，借助牛顿-莱布尼茨公式求解面积！概括说就是：求面积就是求定积分，求定积分就需要求原函数，求原函数就查不定积分表！

为了方便，也把求原函数叫做“求积分”。

说了这么多，π怎么算啊？接下来就是收尾大戏：

为了便于计算，令圆半径为1。此时周长为2π，半周长的大小就是π。因为圆是对称的，只需算出圆周长的四分之一，再乘以2就是半周长，也就是π。

因为x的取值范围是0到1(半径为一），因此圆四分之一周长就是

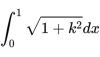
刚才我们说了，k就是圆在某点的导数。因为圆的方程是

y2+x2=1

四分之一的圆的方程（x、y都大于0）就是

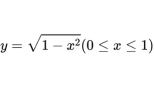
根据求导公式，得出导数

代入k得

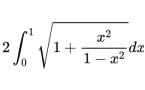
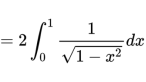
=2(F(1)-F(0))

根据不定积分表，

arcsin(x)是正弦函数的反函数，就是把正弦函数的x和y颠倒过来，比如sin(π/2)=1,则arcsin(1)=π/2（π/2就是90度）。

因此，

2(F(1)-F(0))

=2arcsin(1)-2arcsin(0)

=2（π/2)

=π

因此，我们用微积分方法，也能算出圆周率！

我们从割圆术出发，讨论了微积分的几个重要部分：极限、微分学、积分学。最后用微积分重新算出了圆周率。

下面回顾一下：

割圆术的实质，是用短小的直边逼近圆周的曲线。当我们把圆周无限细分，可以把几乎看不出弯曲的短曲线看成直线。然后把这些直线的长度求和，就相当于圆的周长。

这里面有两个过程。第一个是切割：在圆内作越来越短的割线，割线最后会成为与圆只有一个交点的切线，把这段非常短小的切线长代替局部的曲线长。切线的斜率叫“导数”。

第二个过程是把这些细微的短线求和，积少成多，求割线趋于0时的极限，称为“积分”。

不论微分还是积分，都必须有一个前提：曲线必须是完整的，不可以有缺口——因为直线与缺口没有交点，就没有切线。换句话说，曲线必须连续！因此，连续是微分、积分的前提。把有限的长度切分成一系列细微部分，用越切越细的过程逼近结果，是微分、积分的基础。

参考文献：

[1]常庚哲,史济怀编.数学分析教程.上册[M].北京：高等教育出版社,2003.5

[2][日]小平邦彦著;裴东河译.微积分入门[M].北京：人民邮电出版社,2019.3

来源: 陈林孝