提到“消消乐”，相信很多人都会会心一笑。这款简单又上瘾的手机小游戏，陪伴了我们无数个“碎片化”闲暇时光——不过呢，我除了睡觉做梦之外，其他绝大部分时间都已被手机“碎片化”了！

你知道吗？消消乐，不只是游戏的那么简单！背后的逻辑其实与一种叫做“元胞自动机”的深奥计算机算法有着千丝万缕的联系呢！

消消乐，究竟与元胞自动机有何不解之缘？元胞自动机，这位来自数学与计算机科学领域的“神秘嘉宾”，又与生物力学有何瓜葛呢？今天，就让我们一起踏上这场跨越学科的奇妙旅途，探寻消消乐与元胞自动机之间的趣味联系，以及元胞自动机在生物力学中的奇妙应用。

一、消消乐游戏与元胞自动机的“不解之缘”

首先来了解一下这两个好像“八竿子打不着”的主角。

消消乐（Anipop）是一款益智游戏，其基本玩法非常简单，基本原理是通过消除相同的方块来获得积分。玩家需要在有限的时间内，通过交换相邻的两个方块，使相同颜色的方块连成特定的结构（如一行、一列或正方形等），从而消除这些方块并得分（图1）。随着游戏的进行，新的方块会不断从下方或两侧生成，增加游戏的难度和挑战性。玩家需要观察和计划移动策略，找出可以形成消除的特定方块组合，并尽量避免形成无法消除的结构。

图1 消消乐，乐逍遥

元胞自动机（Cellular Automata，简称CA），中文也译作细胞自动机、点格自动机、分子自动机或单元自动机，是一种时间、空间、状态都离散的，空间相互作用和时间因果关系为局部的网格动力学模型（不好理解，后面详解）。它由许多简单的、遵循相同规则的元胞组成，这些元胞在离散的时间步长上按照规则更新自己的状态，从而模拟出复杂的系统行为。

元胞自动机将连续的空间划分为有限大小的网格，每个网格称为一个元胞。每个元胞可以处于有限种状态之一，这些状态可以用离散的数值表示。根据当前时刻所有元胞的状态，按照一定的规则计算出下一个时刻所有元胞的状态。将时间划分为一系列离散的时刻，每个时刻对应一次状态更新（图2）。

图2 元胞自动机示例

是不是不好理解？好吧，我举个不很恰当、但更容易理解的例子。当你在拥挤的人群中穿行的时候，你就是一个离散网格中的一个“元胞”，你可能会采取如下的规则来行走：当你前面畅通无阻的时候，你自然会往前走；当你前面被一个大胖子挡住去路的时候，你可能选择从旁边绕行；当你感觉疲惫或者遇到红灯的时候，你就停下脚步；当你想起来什么事情的时候，你可能后退返回；当你遇见志同道合者的时候，你会和他们组团而行；当你身边有个美女路过的时候，你就紧紧跟随美女的步伐节奏，如果有缘，你们还可能喜结连理——有情人终成家属；当你看看老人跌倒的时候，你在“扶”与“不扶”间犹豫良久……总之，这些规则对于人群中的每个行人都是同样约定的。那么人群会呈现什么样的动态队形状态呢（图3）？这就是元胞自动机模型算法要处理的问题。

图3 人群的流动

接下来，我们来看看上述两个主角之间的联系。

消消乐与元胞自动机在原理上的联系主要体现在，它们都是基于一定的规则对离散的空间和时间进行迭代更新。

在消消乐中，每个方块其实可以看作是一个元胞。这些方块（元胞）按照一定的规则（即消除规则）进行状态更新。当相同颜色的方块连成一行或一列时，它们就会被消除（即状态更新为“无”），同时释放出新的方块（即状态更新为“有”）。这个过程与元胞自动机中元胞的状态更新过程有着惊人的相似性。

具体来说：（1）离散性：两者都采用了离散的空间和时间模型，消消乐中的方块阵列可以视为一种离散的空间网格，而元胞自动机则更明确地定义了离散的空间和时间。（2）规则性：消消乐的消除规则和元胞自动机的演化规则都起到了关键作用。这些规则决定了系统的状态和动态变化。（3）迭代更新：两者都通过迭代更新来模拟系统的演化过程。在消消乐中，玩家通过移动方块来触发消除操作，从而更新游戏状态；在元胞自动机中，每个元胞的状态则根据局部规则进行同步更新。

那位看官一定会想到，还有一款游戏也有类似的原理，那就是“俄罗斯方块”。确实，“俄罗斯方块”与元胞自动机具有类似的原理。“俄罗斯方块”是一款经典的益智游戏，由苏联游戏设计师阿列克谢·帕金诺夫于1984年创造。它的基本原理是通过移动、旋转和摆放各种形状的方块，让它们在游戏区域内堆叠和消除，直到达到一定的得分或挑战目标。俄罗斯方块中元包含了元胞自动机元素。实际上，如果我们把俄罗斯方块中的每个方块看作是一个元胞，那么整个游戏就可以看作是一个二维的元胞自动机。在元胞状态、邻居关系、状态更新规则等方面，“俄罗斯方块”与元胞自动机在核心原理上却有着惊人的相似性。这种相似性主要体现在它们都是基于一系列简单的规则来模拟和展现复杂系统的行为，体现了离散的空间和时间、简单的规则产生复杂的行为以及并行计算等核心思想。

说完了消消乐游戏与元胞自动机的“不解之缘”，我们接下来进一步了解元胞自动机。

二、进一步了解元胞自动机

1. 元胞自动机的起源故事

元胞自动机的起源故事可以追溯到20世纪中期，与计算机科学的先驱们对复杂系统和自我复制机制的探索紧密相关。在20世纪40年代至50年代，随着计算机科学的兴起，科学家们开始探索如何利用计算机模拟和解释自然界中的复杂现象。其中，自我复制机制是一个备受关注的研究方向，因为它涉及到了生命的基本特征之一。它由约翰·冯·诺依曼创始，经数学家约翰·何顿·康威、物理学家斯蒂芬·沃尔夫勒姆等关键人物的贡献后迅速发展。

先说美国科罗拉多大学的一位数学家，斯塔尼斯拉夫·马尔钦·乌拉姆（Stanislaw Marein Ulam），他在与冯·诺依曼的讨论中提出了一个有趣的问题：是否存在一种简单的规则，能够使得一个系统在没有外部干预的情况下自我复制？这个问题激发了冯·诺依曼对自我复制机制的深入研究。

约翰·冯·诺依曼（John von Neumann）是普林斯顿大学高等研究院教授，是计算机科学的奠基人之一，他在乌拉姆的启发下开始探索自我复制机制的实现。冯·诺依曼认为，如果能够通过简单的规则模拟出自我复制的现象，那么这将为理解生命的本质提供新的视角。冯·诺依曼提出元胞自动机也不仅仅是想窥探生命的奥秘，而更想探究宇宙的终极原理。冯·诺依曼最初提出的元胞自动机模型是一个二维的网格系统，每个网格点代表一个元胞。元胞的状态可以是“生”或“死”，并且根据周围元胞的状态按照一定的规则进行更新。这个模型虽然简单，但却能够模拟出许多复杂的现象，如自我复制、混沌行为等。

约翰·何顿·康威（John Horton Conway）是普林斯顿大学的数学教授，被称为数学界真正的奇男子、老顽童。他出生于英国利物浦，毕业于剑桥大学，在组合博弈论、数论、群论等多个领域都颇有建树。康威对很多游戏都做了数学化的研究，是知名计算机程序“生命游戏”的缔造者。这款程序模拟和显示的图像看起来颇似生命的出生和繁衍过程而得名为“生命游戏”（参见前面的图2）。

斯蒂芬·沃尔夫勒姆（Stephen Wolfram）是普林斯顿大学的计算机科学家、物理学家，提出了“世界的本质就是计算”这一核心观点。他认为，类似元胞自动机这样的计算模型可能是宇宙结构的基础，即宇宙本身是一个巨大的计算系统，宇宙中的物理现象是基于离散的计算过程演化出来的，自然界的复杂可以用元胞自动机的简单计算规则得到。他的著名作品《一种新科学》提到，元胞自动机将取代之前用数学方程来描述世界的方法，这将导致一场科学革命。

2. 康威生命游戏

康威生命游戏（Conway's Game of Life），又称康威生命棋，可以说是最典型的元胞自动机应用案例。它没有玩家，却在学术玩家圈子里风靡全球、火了近半个世纪！

康威生命游戏是一种零玩家游戏，其发展完全由初始状态决定，不需要进一步的输入。玩家可以创建初始配置并观察其演变过程。游戏基于元胞自动机理论，通过简单的规则模拟生命的出生、繁衍和消亡过程。试图在计算机上仿真、合成和生物有机体相关联的一些基本现象，如自我复制、寄生、竞争、进化、协作等，并研究和观察“可能的生命现象”，从而使人们能够加深理解“已知的生命现象”。它使用了一个理论上可以无穷大的二维矩形栅格世界，这个世界中的每个方格居住着一个“活着的”或“死了的”细胞。细胞的生死状态根据周围八个方格中细胞的数量来更新，这体现了元胞自动机中基于局部规则进行状态更新的原理（参见前面图2）。它展示了即使是最简单的规则，也能在适当的条件下展现出惊人的复杂性。

游戏规则如下：（1）存活条件：当一个活细胞周围有2个或3个活邻居时，该细胞在下一代保持存活；当一个死细胞周围有3个活邻居时，该细胞在下一代变为存活状态（模拟繁殖）。（2）死亡条件：当一个活细胞周围有少于2个或多于3个活邻居时，该细胞在下一代变为死亡状态；当一个死细胞周围活邻居的数量不是3个时，该细胞保持死亡状态。

尽管游戏规则非常简单，但康威生命游戏能够展示出稳定型、周期型、混沌型和复杂型四种不同的演化行为，程序运行的结果可能是奇妙惊艳的“生命”图案（图4）。

图4 康威生命游戏生成的“生命”图案（如何设置初始状态和规则，才能经过不断演化而生成这样的图案，这是其中的难点）

康威生命游戏在计算科学、人工生命研究、复杂系统模拟等领域具有一定的应用价值。它可以用于研究群体行为、模拟生态系统、测试算法的性能等。游戏中涌现出的各种美丽图案和结构被艺术家用于创作壁纸、绘画、音乐等艺术作品。它证明了即使是最简单的规则，也能在适当的条件下产生复杂而美丽的模式。这款游戏不仅具有科学研究价值，还启发了人们对生命、社会和宇宙的深刻思考。

3. 格子气方法、格子-玻尔兹曼方法与元胞自动机

聊完了游戏，我们来谈点正经事。

元胞自动机在科学研究中的应用也不乏其例。格子气方法、格子-玻尔兹曼方法与元胞自动机之间存在紧密的关系。

（1）格子气自动机(Lattice Gas Automata，简称LGA)

LGA是一种用来模拟液体流动的细胞自动机。LGA的基本思想是，把计算区域分成许多均匀的正六边形（或正方形）的网格——称之为“格子”，用布尔变量（也就是0和1）表示流体粒子在空间格子上的存在与否；那些只有质量无体积的粒子只能在网格点上存在，并沿着网格线在网格间运动。当某一个粒子从某一网格点到邻近的网格点时，有可能和从其他网格点到达该点的粒子相碰撞。LGA具有构造简单、易于并行等突出的优点。通过LGA，可以得出宏观的流体力学控制方程——纳维-斯托克斯（Navier-Stokes）方程。LGA的物理图像简单、直观、易于编程，在粗略模拟流体行为（特别是复杂流体行为）方面发挥着重要作用（图5）。

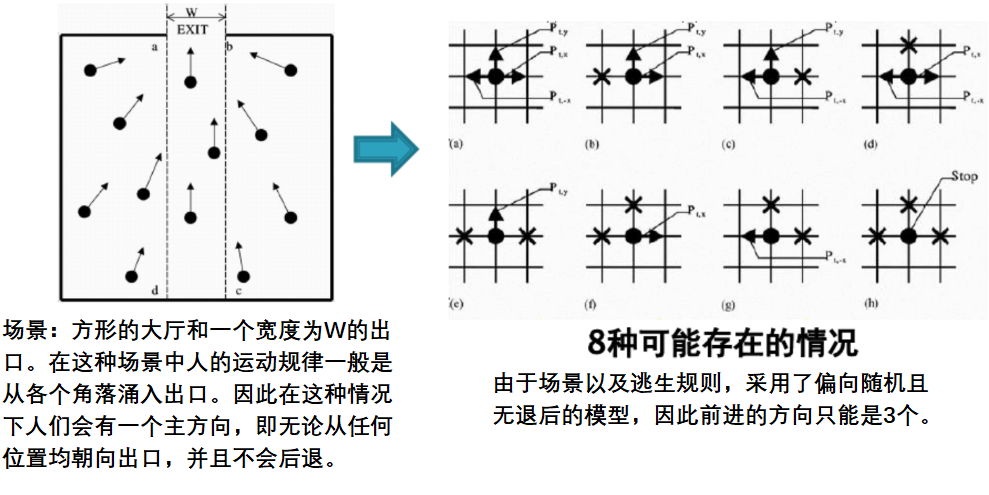
图5 人流运动模拟方法

（2）格子-玻尔兹曼方法（Lattice Boltzmann Method, 简称LBM）

LBM是一种基于介观模拟尺度（是指介于宏观和微观之间的尺度；一般认为它的尺度在纳米和毫米之间）的计算流体力学方法。它是20世纪80年代中期建立和发展起来的一种流场模拟方法，继承了格子气自动机的主要原理并对其作了改进。

LBM通过流体分子的速度分布函数，研究速度分布函数在时间和空间上的演化过程，再根据速度分布函数与边界条件设置的流体运动的宏观物理量之间的关系，从而获得流体运动的宏观信息。

格子玻尔兹曼方程，在空间上流体区域被离散为一系列格子，在计算时间上离散为一系列时间步长，速度也同样被离散。微观流体粒子在永不停息地做无规则热运动（碰撞-迁移），在微观上看流体分子的速度的大小是连续的，速度是矢量，既有大小又有方向，在空间上速度有无数个方向（图6）。

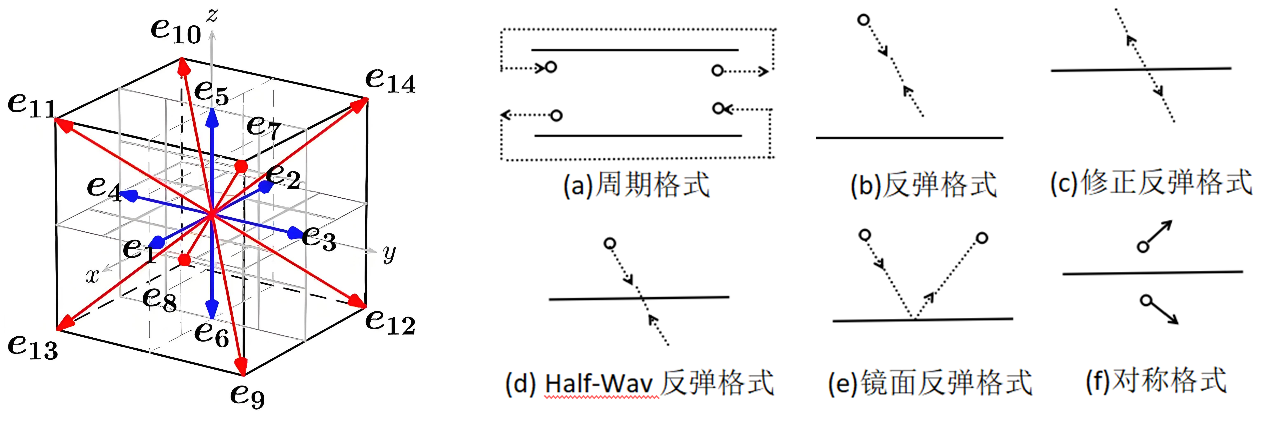
图6 格子模型以及几类启发式边界条件

LBM突破了传统计算方法的理论框架，直接从离散模型出发，应用物质世界最根本的质量守恒、动量守恒和能量守恒规律，在分子运动论和统计力学的基础上构架起宏观与微观、连续与离散之间的桥梁。被广泛地认为是描述流体运动与处理工程问题的有效手段，用于多组分、多相流、界面动力学、化学反应与传递等领域。

从历史的角度看，格子气方法和格子-玻尔兹曼方法都是由元胞自动机模型发展而来。长期以来，描述自然现象的数学模型为微分方程。从20世纪60年代开始，人们开始设想一种称之为“格子气”或“元胞自动机”的离散模型。格子-玻尔兹曼方法则是在格子气自动机模型基础上经过若干主要的演变发展而来的。

这三者之间存在内在的联系：格子气自动机、格子-玻尔兹曼方法与元胞自动机都体现了离散模型的思想，都通过一系列规则来模拟复杂系统的行为。它们在不同领域和尺度上发挥着重要作用，相互借鉴、共同推动了计算科学、物理学、工程学等多个领域的发展。

三、元胞自动机在生物力学中的应用

说完了元胞自动机的“光辉历史”，我们再来聊聊元胞自动机在生物力学领域的应用。

元胞自动机的英文名称中用到了“细胞”这个名词，那么它和细胞分裂演化行为有何关联吗？这个真没有！

从元胞自动机的起源来看，虽然元胞自动机并非直接源于对细胞分裂演化行为的模拟，但细胞分裂和演化的复杂性为元胞自动机提供了灵感。元胞自动机通过简单的规则模拟复杂系统的行为，这与生物系统中细胞通过简单的规则实现复杂的分裂和演化过程有一定的相似性。

后来，元胞自动机在模拟细胞行为方面得到了应用。例如，基于生物细胞生长机理和莫诺德微分方程模型（用于描述微生物比增殖速度与有机底物浓度之间的函数关系），可以推导出生物细胞生长以及底物消耗的微分方程，并基于此建立模拟生物细胞生长的元胞自动机模型。这些模型能够较好地描述细胞生长的演化行为。

1. 细胞生长与分裂的模拟

细胞是生物体的基本组成单位。它们的生长和分裂过程受到多种因素的调控和影响。利用元胞自动机模型，我们可以模拟细胞在不同条件下的生长和分裂行为。例如，利用元胞自动机模型来模拟肿瘤细胞的生长和分裂过程，通过定义不同的元胞状态和更新规则，我们可以模拟出细胞在营养物质充足或缺乏、生长因子存在或缺失等情况下的生长、分裂和扩散过程。结果显示，该模型能够准确地预测肿瘤细胞的生长速度和扩散范围，与实验数据高度一致。

这种模拟不仅有助于我们深入理解细胞生长和分裂的调控机制，还可以为组织工程和再生医学等领域提供有力的支持。例如，在组织工程中，我们可以利用元胞自动机模型来优化生物材料的结构和性能，以促进细胞的生长和分化；在再生医学中，我们可以利用元胞自动机模型来模拟组织修复和再生的过程，为疾病治疗提供新的思路和方法。通过定义不同的元胞状态和更新规则，研究者成功地模拟出了细胞在生物材料表面的附着、增殖和分化过程。实验结果显示，该模型能够准确地预测细胞在生物材料表面的生长情况和分布规律，为组织工程的设计和优化提供了有力的支持。

2. 细胞骨架动态变化的模拟

细胞骨架是细胞内的一种蛋白质纤维网络，它支撑着细胞的形态并参与了细胞的多种功能活动。细胞骨架的动态变化对于细胞的生长、分裂、迁移等行为都具有重要的影响。利用元胞自动机模型，我们可以模拟细胞骨架在不同条件下的动态变化过程。

例如，通过定义不同的元胞状态和更新规则，我们可以模拟出细胞骨架在受到力学刺激或化学信号作用下的重排和重组过程。这种模拟不仅有助于我们深入理解细胞骨架的调控机制，还可以为细胞力学和细胞生物学等领域的研究提供有力的支持。

3. 生物组织力学行为的模拟

生物组织是由多种细胞和细胞外基质组成的复杂系统。它们的力学行为对于生物体的功能和健康都具有重要的影响。利用元胞自动机模型，我们可以模拟生物组织在不同条件下的力学行为。

例如，通过定义不同的元胞状态和更新规则，我们可以模拟出生物组织在受到拉伸、压缩或剪切等力学刺激下的响应和变形过程。这种模拟不仅有助于我们深入理解生物组织的力学性能和调控机制，还可以为生物医学工程、康复医学等领域的研究提供有力的支持。例如，在生物医学工程中，我们可以利用元胞自动机模型来优化医疗器械的设计和使用效果，提高医疗器械的性能和安全性；在康复医学中，我们可以利用元胞自动机模型来评估患者的康复效果和制定个性化的康复方案，提升个性化精准医疗水平。

4. 基于代理模型与血管重塑的模拟

基于代理模型（Agent-Based Modeling, 简称ABM），也称为基于个体模型、多元代理系统等，与元胞自动机类似，都是模拟复杂系统动态行为的重要工具，关注系统的组成部分及其相互作用。ABM中的模拟个体对象称作代理，代理在模拟过程中根据定义的规则执行相应的行为，包括自身独立的行为以及与其他代理的相互作用。它通过模拟代理的行为和相互作用，来研究系统整体的动态变化。

就比如我们都遇到过上下班高峰期的交通拥堵问题。通过ABM模型，我们可以模拟每一辆车（代理）的驾驶行为和相互作用。模型中，每辆车都有其速度、加速度等属性，以及遵守交通规则的行为规则。通过模拟，研究者可以发现哪些因素（如交通信号灯设置、车流量等）会导致拥堵，并提出优化方案。

在血管重塑方面，ABM广泛用于模拟内皮细胞（EC）、血管平滑肌细胞（VSMC）以及细胞外基质（ECM）等成分的活动。血管壁由内膜、内弹性层、中膜、外弹性层、外膜等结构组成（图7）。

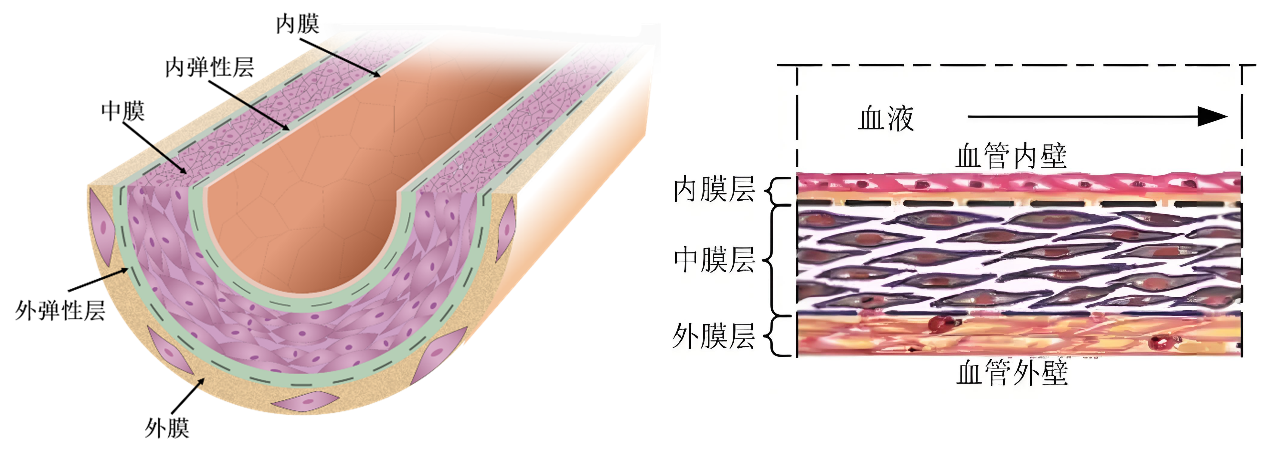
图7 血管壁结构示意图

内膜由一层扁平EC构成，中膜由VSMC构成，外膜由成纤维细胞构成。ECM对细胞起到复杂网络支持物的作用，并且作为一个关键的生物化学和生物力学信号来源，参与控制细胞的生长、形状、迁移、稳定和代谢活动。

血管重建是一个力学-化学-生物学共同作用的过程。在血管重塑的ABM中，每个代理可以代表血管壁上的一个细胞（如EC、VSMC等）。这些代理根据预设的规则和环境因素（如血流切应力、血压、血管壁张应力、生长因子浓度等）进行决策和行动。代理之间的相互作用可以模拟细胞间的信号传导、物质交换等过程。

科学家在模拟VSMC分裂/凋亡、ECM降解/合成过程中，考虑了壁面切应力（WSS）、生化因子、VSMC和ECM之间的相互作用。其中生化因子包括内皮素(endothelin, ET)、NO和基质金属蛋白酶-9(matrix metalloproteinases-9, MMP-9)等。根据文献建立了WSS、生化因子含量、VSMC和ECM之间的数学关系，并且根据血管内支架植入后血管壁的受力状况模拟了血管重塑过程（图8）。

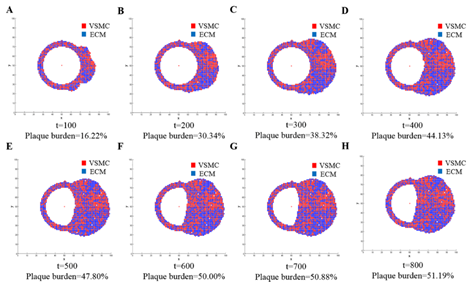
图8 ABM模拟血管重塑的横截面形状变化过程，这一过程再现了随着血管重塑时间增长、血管壁正性重塑何负性重塑的情形。

利用ABM的血管重塑模型，可以研究血管在高血压、动脉粥样硬化等病理条件下的重塑机制，以及支架介入治疗后的血管重塑过程。ABM通过模拟不同条件下的血管重塑过程，可以展现血管动态与血管稳态的分子、细胞机理，揭示血管重塑的关键驱动因素和潜在的治疗靶点，还可以用于评估不同治疗策略对血管重塑的影响，为临床决策提供科学依据。

四、结语

从 “消消乐”游戏到元胞自动机，再到格子-玻尔兹曼方法和基于代理模型，可以说是一场跨越学科的奇妙旅行，带我们了解了科学知识无处不在及其奇妙之处。

通过今天的探讨，我们不难发现消消乐与元胞自动机之间竟然存在着如此紧密的联系。而元胞自动机这位来自数学与计算机科学领域的“神秘嘉宾”，在生物力学领域也发挥着如此重要的神奇作用。这场跨越学科的奇妙邂逅不仅让我们对消消乐和元胞自动机有了更深入的了解，也让我们看到了跨学科研究的无限可能。

在未来的日子里，我们期待着更多的跨学科研究能够涌现出来，为我们揭示自然界的奥秘和推动人类社会的进步贡献更多的智慧和力量。同时，我们也期待着消消乐这样的简单小游戏能够继续带给我们欢乐和启发，让我们在娱乐的同时也能感受到科学的魅力和力量。

科学之美，无处不在，就看你是否能玩出新花样。

同样的东西，我能玩的是游戏，别人玩的是科技。

来源: 医用生物力学