上一节我们创建了算术逻辑单元ALU，它可以进行算术、逻辑运算，但计算出来的结果如何保存呢？这就需要用到存储单元，接下来我们看看用什么电路能够保存数据。

由浅入深，我们先来存储1位二进制数。先看这个改造过的或门电路。

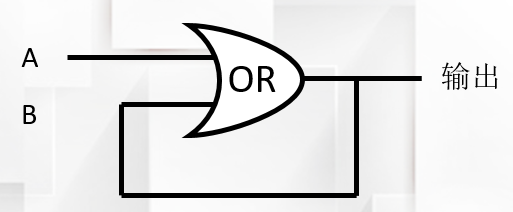
它的特殊之处在于其输出信号会作为输入信号之一，看起来很奇怪是吧。一开始A、B都为0，输出=0，当A=1时或门输出=1，那么B=1，这时A、B都是1，输出还是1，保持不变，接下来即使将A设为0，输出依然是1。于是这个电路可以保存信号1。但我们也会发现一个问题，即这个保存是永久性的，不论A的值是什么，输出都是1，这显然不符合实际需求，保存的数据应该可以修改才对，这个问题暂时放一放，后面再解决。

接下来我们再看这个改造过的与门电路，同样它的输出信号也作为输入信号之一。

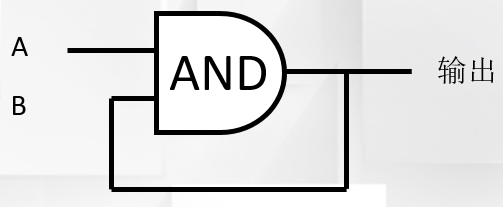
一开始将A、B都设为1，输出=1，当A设为0时，输出=0，进而B=0，输出还是0，保持不变。接下来不论A如何变化，输出始终保持为0，所以这个电路可以保存0。

然后我们开始着手解决如何修改保存内容的问题，设计如下电路：

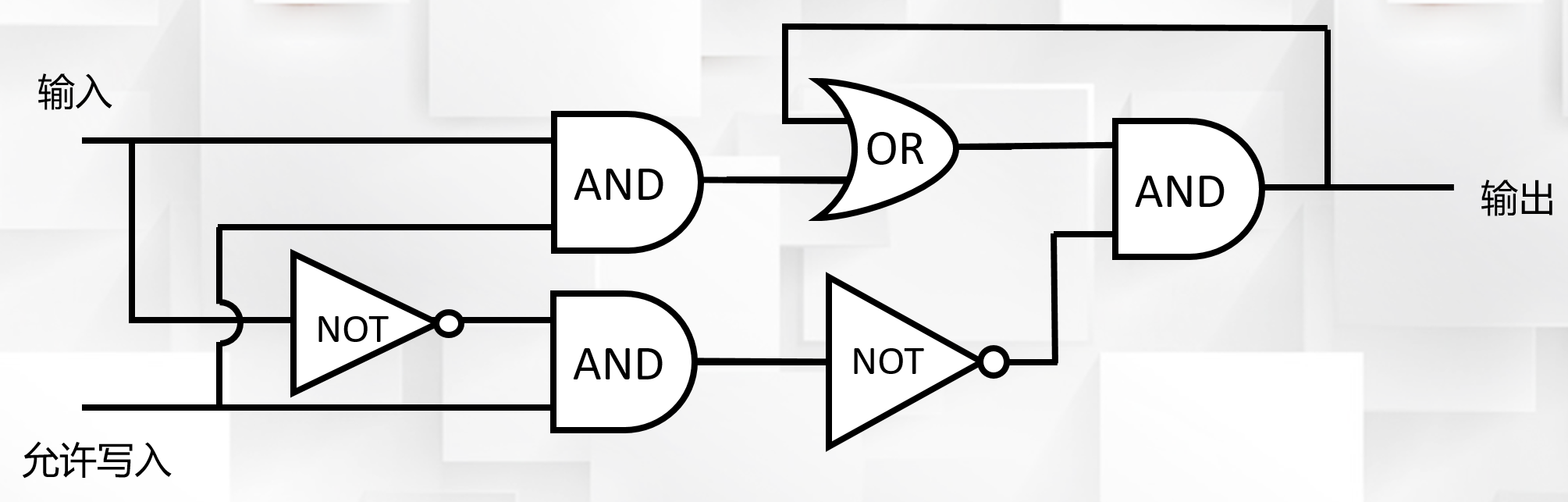
其中“输入”端的信号就是这个电路要保存的值，“允许写入”代表是否可以修改保存值，如果是0，代表不能修改，如果是1，代表可以修改，“输出”端的信号就是保存的值。这个电路大家可以自行分析，我将四种不同的情况列在下面供大家参考。

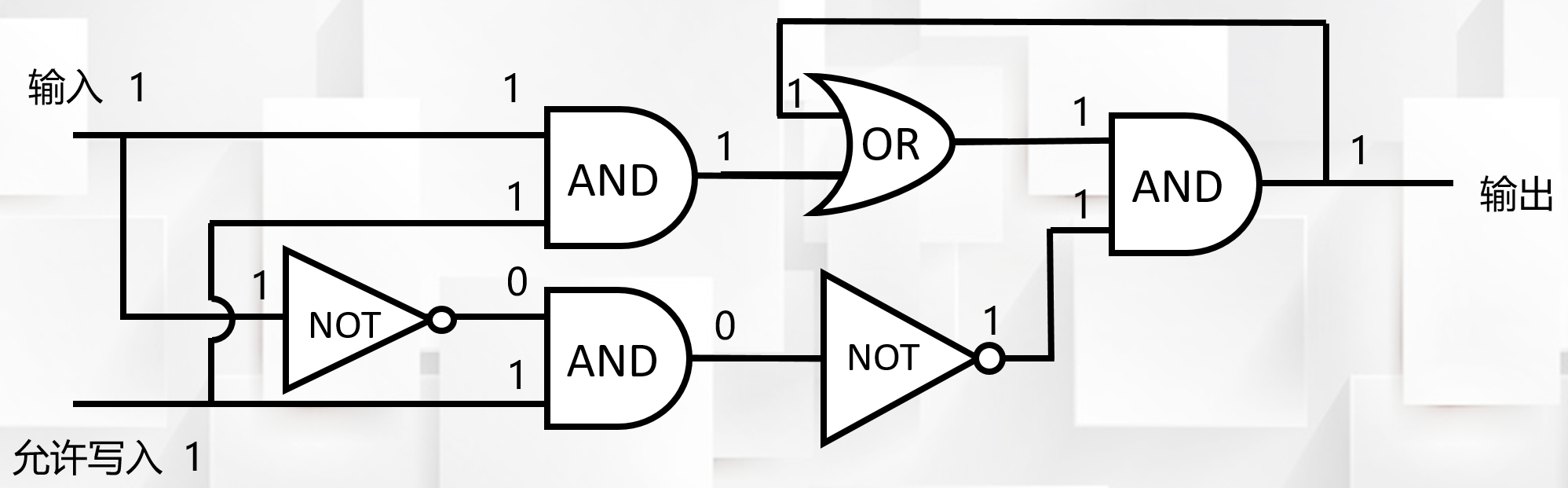
允许写入情况，输入端信号1会保存起来

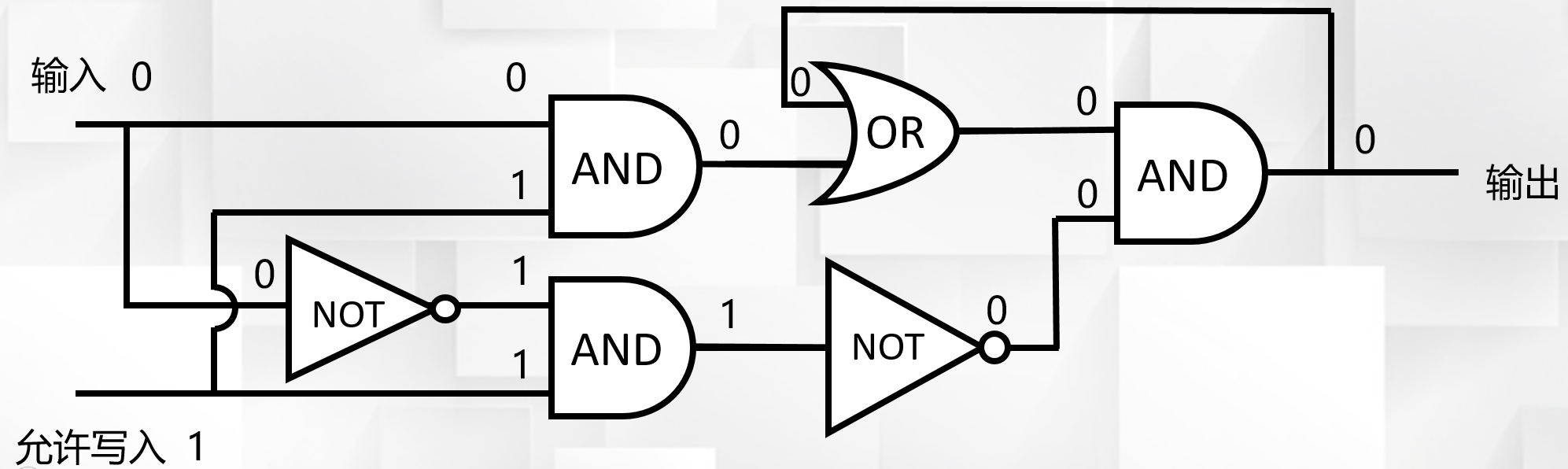
允许写入情况，输入端信号0会保存起来

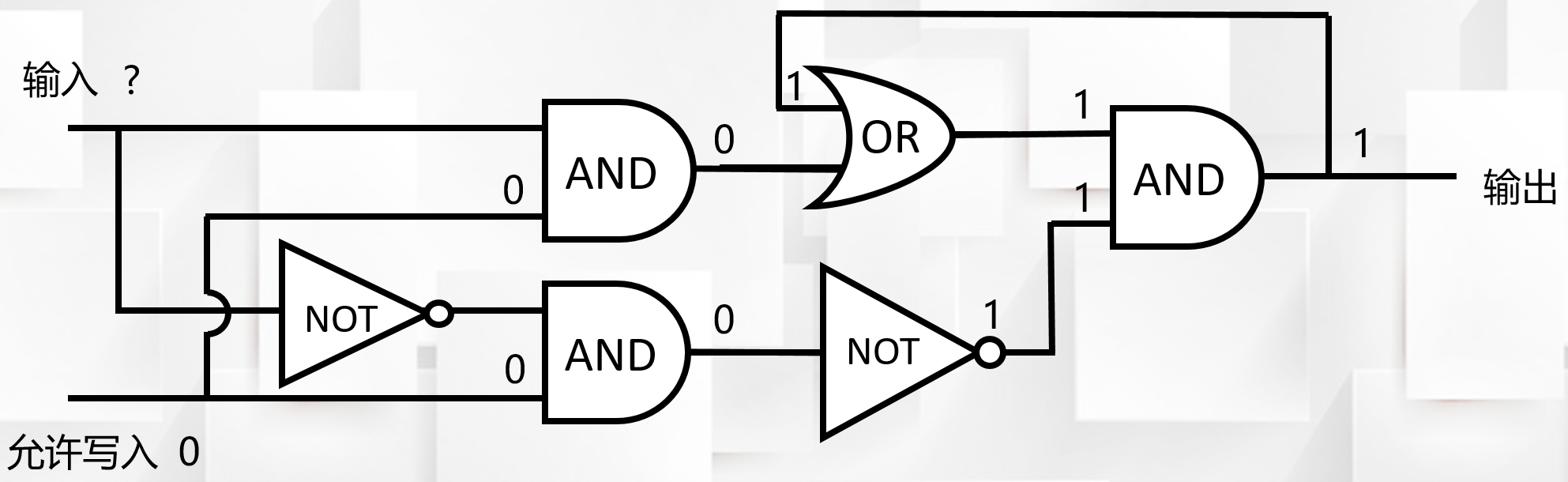
禁止写入情况，电路原本保存1，不论输入端是什么都没有影响

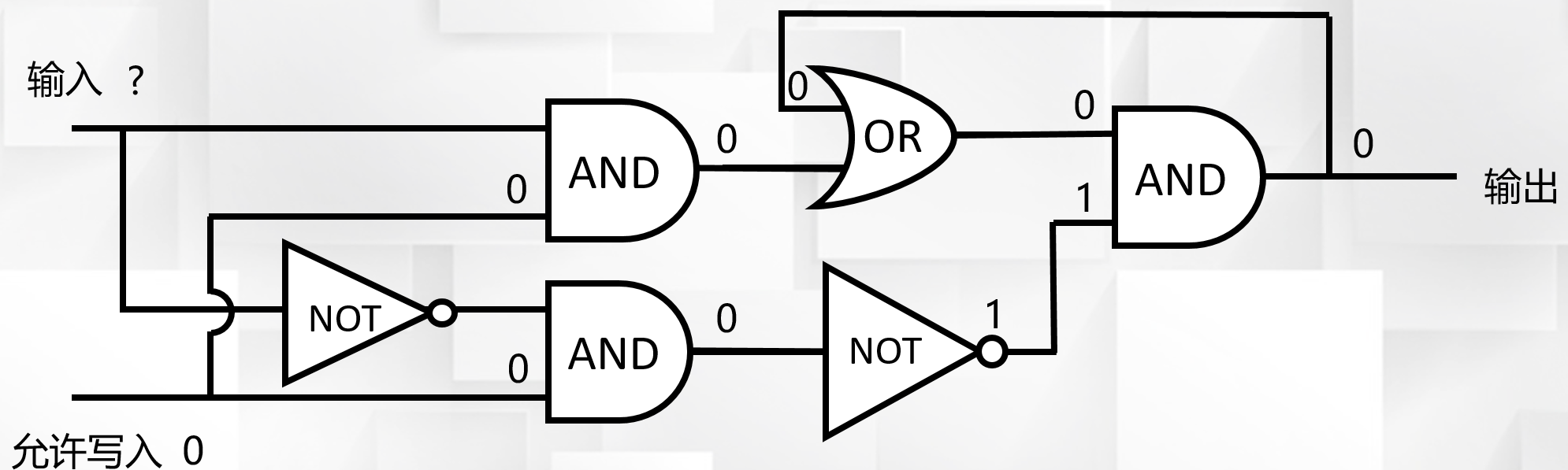
禁止写入情况，电路原本保存0，不论输入端是什么都没有影响

我们用一个简化的符号代替这个电路，这个电路可以保存1位二进制数，并且可以随意修改，我们把它叫做锁存器。

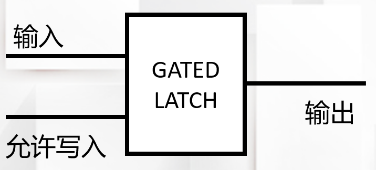
当我们将8个锁存器放在一起，就可以保存8位二进制数了，这样一组锁存器被称为寄存器。早期电脑使用8位寄存器，即由8个锁存器组成，能保存8位二进制数，后来出现了16位寄存器、32位寄存器，到现在的电脑基本都是64位寄存器了。

接下来我们设计一个能存储256位二进制数的电路，如下图：

我们共需要16*16=256个锁存器，将他们设计成16行16列的矩阵，为了能准确存取数据，我们需要知道每个锁存器的位置，所以需要一个额外的电路确定要操作的锁存器的地址。如果要确定地址，必须知道行数、列数，一共16行、16列，所以行和列各用4位二进制数表示就行（0000代表第1行，0001代表第2行……，1111代表第16行，列也是一样的），这样就需要8位的地址输入信号。受篇幅所限，细节的电路不再画了，最终我们有了一个能存取256位二进制数的电路，用这个图形表示。

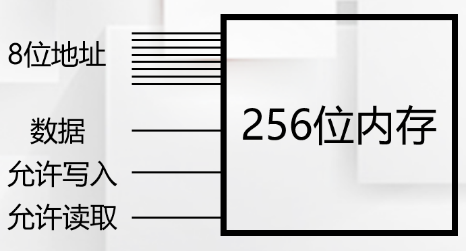
“8位地址”用于定位锁存器的位置，“允许写入”=1时，“数据”被存入某个锁存器，“允许读取”=1时，某个锁存器的数据可以被读取出来。

一个这样的电路还是没什么卵用的，还需要继续扩大规模，我们将8个相同的电路如图所示连接在一起。

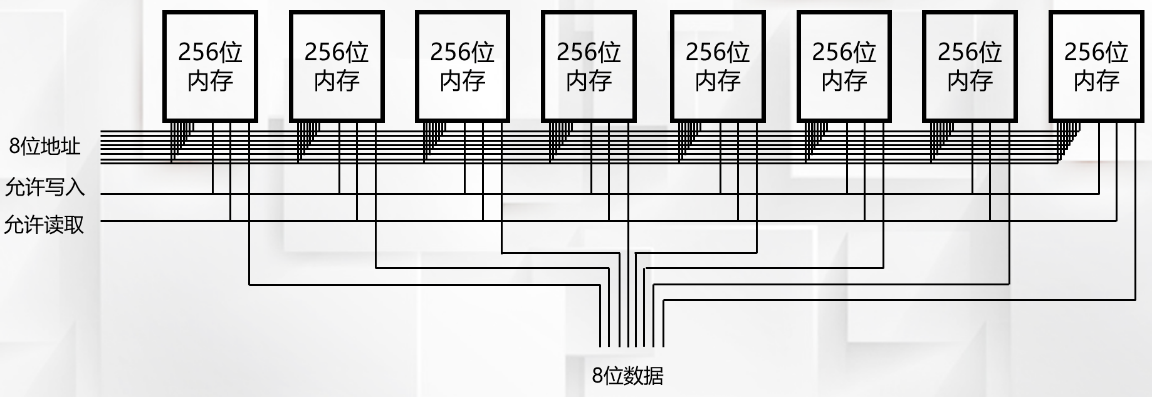
这样我们一次就可以读写8位二进制数了，8位也叫做一个字节（Byte，简称B）。同样，我们简化一下，使用下图表示。

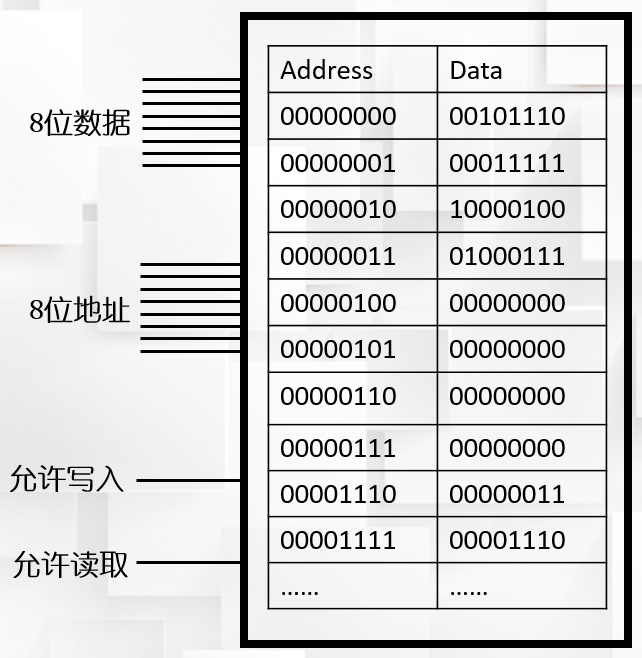
这个电路有256个地址，每个地址可以读写一个8位二进制数，一共可以保存256个字节（256B）的数据。这个容量的存储空间能够保存什么呢？很遗憾，现在的文档、图片动辄以KB、MB为单位，似乎什么也干不了。

补充一下小知识，1GB=1024MB，1MB=1024KB，1KB=1024B。

至此我们使用多个锁存器构建出了可以存取数据的内存，虽然只有256B，更大的内存也是同样的原理，下节我们就开始打造完整的CPU了！

来源: 孙老师聊人工智能