概念
如图1所示为一曲柄摇杆机构,设曲柄AB为原动件,在其转动一周的过程中,有两次与连杆共线,这时摇杆CD分别处于两极限位置C1D和C2D。机构所处的这两个位置称为极位。机构在两个位置时,原动件AB所在两个位置之间的夹角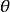 称为极位夹角。1
称为极位夹角。1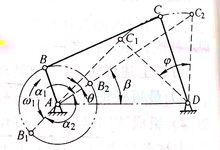
四杆机构的急回运动和极位夹角急回运动的出现如图1所示,当曲柄以等角速度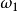 顺时针转过
顺时针转过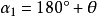 时,摇杆将由位置
时,摇杆将由位置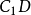 摆到
摆到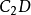 ,其摆角为
,其摆角为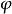 ,设所需时间为
,设所需时间为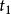 ,
,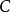 点的平均速度为
点的平均速度为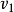 ;当曲柄继续转过
;当曲柄继续转过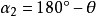 时,摇杆又从位置
时,摇杆又从位置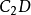 回转到
回转到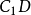 ,摆角仍然是
,摆角仍然是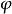 ,所需的时间是
,所需的时间是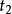 ,
,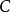 点的平均速度为
点的平均速度为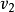 。由于曲柄为等角速度转动,而
。由于曲柄为等角速度转动,而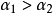 ,所以有
,所以有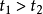 ,
,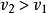 。摇杆这种性质的运动称为急回运动。1
。摇杆这种性质的运动称为急回运动。1
急回运动的衡量为了表明急回运动的急回程度,可用行程速度变化系数或称行程 系数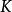 来衡量,即:
来衡量,即:
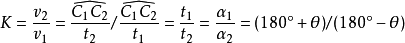 上式表明,当机构存在极位夹角
上式表明,当机构存在极位夹角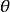 的时候,机构便具有急回运动特性,
的时候,机构便具有急回运动特性,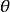 角越大,
角越大,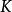 值越大,机构的急回运动性质也越明显。1
值越大,机构的急回运动性质也越明显。1
判断是否存在急回运动判断机构是否存在急回运动:
(1)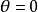 无急回运动
无急回运动
(2)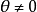 有急回运动
有急回运动
急回特性在工程上的应用机构的急回特性在工程上有三种应用情况:
(1)工作行程要求慢速前进,以利切削、冲压等工作的进行,而回程时为节省空间时间,则要求快速扳回,如牛头刨床、插床等就是如此,这是常见的情况。
(2)对某些颚式破碎机,要求其颚快进慢回,使以被破碎的矿石能及时推出颚板,避免矿石的过粉碎(因破碎后的矿石有一定粒度要求)。
(3)一些设备在正、反行程中均在工作,故无急回运动。某些机载搜索雷达的摇头机构就是如此。1
有急回运动的机构的设计在设计时,应先明确行程速度变化系数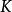 ,求出
,求出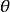 角后,再设计各杆的尺寸。1
角后,再设计各杆的尺寸。1
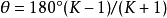
曲柄摇杆机构设计示例按给定的行程速比系数设计
在设计需要有急回特性的四杆机构时,常按实际要求先给定行程速比系数 K,再根据机构在极限位置的几何关系及有关辅助条件,设计出机构各构件的位置和尺寸。
已知:如图2所不,摇杆长度CD,摇杆摆角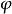 ,行程速比系数
,行程速比系数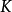 。求:确定铰链A的位置,并定出A 、BC 、AD 三杆长度。
。求:确定铰链A的位置,并定出A 、BC 、AD 三杆长度。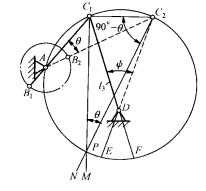
如图2所示,任选一点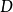 ,由已知
,由已知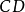 杆长和摆角
杆长和摆角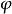 画出其两极限位置并得到
画出其两极限位置并得到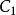 、
、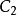 铰链点。连接
铰链点。连接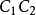 再作
再作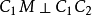 。由已知的
。由已知的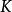 代入式
代入式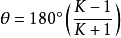 计算出极位夹角
计算出极位夹角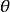 。作
。作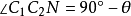 。
。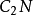 与
与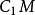 交于
交于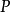 点。由
点。由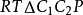 三个内角之和为180°可知,
三个内角之和为180°可知,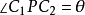 。作
。作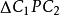 的外接圆,在除
的外接圆,在除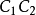 和
和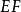 外的圆弧上任选一点
外的圆弧上任选一点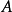 作为固定铰链点。连接
作为固定铰链点。连接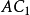 和
和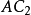 得夹角
得夹角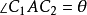 (同一圆周角相等)。因两极限位置处曲柄
(同一圆周角相等)。因两极限位置处曲柄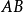 和连杆
和连杆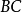 共线,故可得
共线,故可得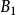 在
在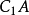 的延长线上,
的延长线上,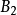 在
在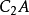 线之间。先初取
线之间。先初取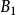 、
、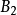 点并使
点并使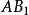 和
和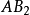 相等。由其几何关系应得
相等。由其几何关系应得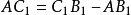 ,
,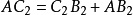 ,于是得到曲柄
,于是得到曲柄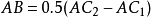 。再以
。再以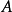 为圆心
为圆心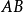 为半径作圆,交
为半径作圆,交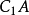 的延长线于正式取得的
的延长线于正式取得的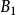 点,交
点,交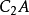 线上于正式取得的
线上于正式取得的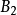 点。
点。
因 A点是在外接圆上任取的一点,故此题的结果可有无穷多。如果要取得良好的传动质量,可再按照最小传动角最优或其他辅助条件来最终确定 A的位置。2
导杆机构设计示例按给定的行程数比设计
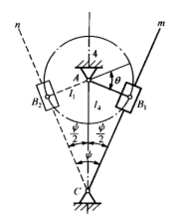 已知:如图3所示,机架长度AC ,行程速比系数 。求:AB杆长度。
已知:如图3所示,机架长度AC ,行程速比系数 。求:AB杆长度。
由已知的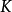 代人式中计算出极位夹角
代人式中计算出极位夹角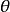 。在四边形
。在四边形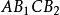 中,因
中,因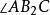 和
和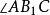 恒为直角,故
恒为直角,故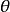 和导杆摆角
和导杆摆角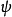 均与
均与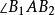 互补,故驴
互补,故驴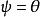 。现任选一点作固定铰链
。现任选一点作固定铰链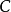 ,以摆角
,以摆角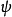 作出导杆的两个极限位置
作出导杆的两个极限位置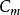 和
和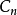 。作
。作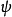 的角平分线
的角平分线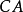 ,
,
并取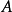 点使
点使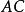 等于已知的机架长度。再过
等于已知的机架长度。再过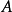 点作导杆两极限位置
点作导杆两极限位置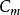 和
和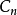 的垂线,分别交于
的垂线,分别交于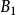 、
、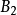 点。于是得到
点。于是得到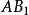 ,或
,或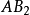 即为曲柄的长度。2
即为曲柄的长度。2


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

