常值函数(constant function)指值域为一元集的函数,当它为数值函数时常以f(x)=const或f(x)=c表示,这里的const与c都是constant(常数)的简写,在xy坐标平面上,函数f(x)=c的图象是直线y=0。换句话说,常值函数是其值域仅含一个元素的函数。即对该函数定义域中的一切x,都有f(x)=a,其中a是一个固定元素。
基本介绍把常量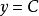 (
(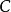 为常数)定义为函数,通常是这么理解的:不论自变量
为常数)定义为函数,通常是这么理解的:不论自变量 取什么样的实数值,因变量
取什么样的实数值,因变量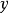 恒取常值
恒取常值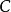 ,所以常值函数
,所以常值函数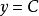 的定义域
的定义域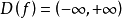 ,值域
,值域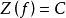 。它的图像是一条平行于
。它的图像是一条平行于 轴并通过点
轴并通过点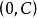 在
在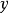 轴上截距为
轴上截距为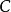 的直线(如图1所示)。常值函数的特点是不显含自变量且不存在反函数1。
的直线(如图1所示)。常值函数的特点是不显含自变量且不存在反函数1。
常值函数的周期性常值函数是一个周期函数。因对于任何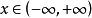 和实数
和实数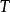 ,
,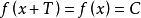 ,但并无最小正周期1。
,但并无最小正周期1。
常值函数的导数常值函数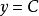 (
(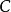 为常数)的导数
为常数)的导数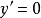 。
。
**证:**对于函数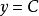 ,当自变量在任意点
,当自变量在任意点 处取改变量
处取改变量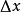 时,
时,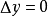 恒成立2。
恒成立2。
于是
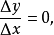 所以
所以
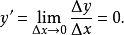
常值函数因变量与自变量常值函数因变量是固定的,即无论自变量取什么值其函数值(因变量)都不会发生变化。因此,实际上常值函数也有自变量,例如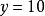 也可以写成
也可以写成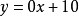 。在没有任何其它限制的情况下,
。在没有任何其它限制的情况下, 可以取任何值,即全体实数。
可以取任何值,即全体实数。
在部分文献中,将常值函数视为0次函数,即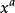 当
当 时,在
时,在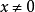 的情况下,恒等于1。但由于0次幂要求
的情况下,恒等于1。但由于0次幂要求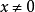 ,而常数函数允许
,而常数函数允许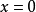 ,所以也有些文献不赞成将常数函数视为0次函数。
,所以也有些文献不赞成将常数函数视为0次函数。
周期函数的定义对于函数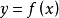 ,若存在常数
,若存在常数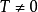 ,使得f(x+T) = f(x),则函数
,使得f(x+T) = f(x),则函数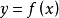 称为周期函数,T称为此函数的周期。
称为周期函数,T称为此函数的周期。
性质1:若T是函数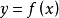 的任意一个周期,则T的相反数(-T)也是
的任意一个周期,则T的相反数(-T)也是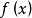 的周期。
的周期。
性质2:若T是函数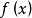 的周期,则对于任意的整数n(n≠0),nT也是
的周期,则对于任意的整数n(n≠0),nT也是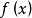 的周期。
的周期。
性质3:若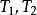 都为函数
都为函数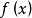 的周期,且
的周期,且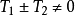 ,则
,则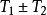 也是
也是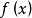 的周期。
的周期。
在函数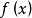 的周期的集合中,我们称其正数者为函数
的周期的集合中,我们称其正数者为函数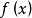 的正周期,称其负数者为函数
的正周期,称其负数者为函数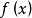 的负周期。若所有正周期中存在最小的一个,则我们称之为函数
的负周期。若所有正周期中存在最小的一个,则我们称之为函数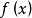 的最小正周期,记作T*。
的最小正周期,记作T*。
补充:常值函数无单调性。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

