基本概念直观地讲,对于平面上的n个点,把其中的一些点对用曲线或直线连接起来,不考虑点的位置与连线曲直长短,这样形成的一个关系结构就是一个图。记成G=(V,E),V是以上述点为元素的顶点集,E是以上述连线为元素的边集。
如果图的两顶点间有边相连.则称此两顶点相邻,每一对顶点都相邻的图称为完全图,否则称为非完全图.设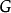 为n阶无向简单图,若
为n阶无向简单图,若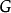 中每个顶点均与其余的
中每个顶点均与其余的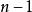 个顶点相邻,则称
个顶点相邻,则称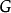 为n阶无向完全图,简称n阶完全图,记做
为n阶无向完全图,简称n阶完全图,记做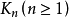 。设
。设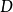 为n阶有向简单图,若
为n阶有向简单图,若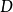 中每个顶点都邻接到其余的
中每个顶点都邻接到其余的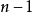 个顶点,又邻接于其余的
个顶点,又邻接于其余的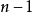 个顶点,则称
个顶点,则称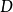 是n阶有向完全图。
是n阶有向完全图。
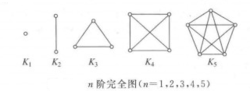
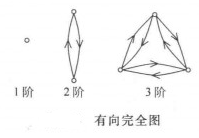
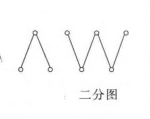
图1分别列出了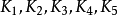 。图2分别列出了1阶有向完全图、2阶有向完全图、3阶有向完全图。
。图2分别列出了1阶有向完全图、2阶有向完全图、3阶有向完全图。
若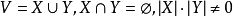 (这里
(这里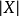 表示顶点集
表示顶点集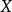 中元素的个数),且
中元素的个数),且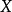 中无相邻的顶点对,
中无相邻的顶点对,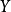 中亦然,则称图
中亦然,则称图 为二分图;特别地,若对任意
为二分图;特别地,若对任意 ,
, 与
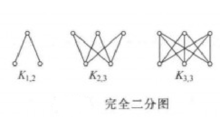
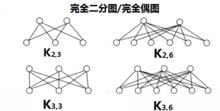
与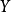 中每个顶点相邻,则称图G为完全二分图(complete bipartite graph),或称完全偶图,记为
中每个顶点相邻,则称图G为完全二分图(complete bipartite graph),或称完全偶图,记为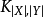 。1
。1
相关概念图G=(V,E)各条边都加上方向的图称为有向图,否则称为无向图。如果有的边有方向,有的边无方向,则称为混合图。
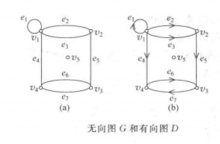
任两顶点间最多有一条边,且每条边的两个端点皆不重合的图,称为简单图。
设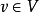 是边
是边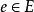 的端点,则称v与e相关联,与顶点v关联的边数称为该顶点的度,记为
的端点,则称v与e相关联,与顶点v关联的边数称为该顶点的度,记为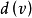 ,度为奇数的顶点称为奇顶点,度为偶数的顶点称为偶顶点。可以证明
,度为奇数的顶点称为奇顶点,度为偶数的顶点称为偶顶点。可以证明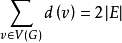 ,即所有顶点的度数之和是边数的2倍,且由此可知奇顶点的总数是偶数。
,即所有顶点的度数之和是边数的2倍,且由此可知奇顶点的总数是偶数。
设 ,其中
,其中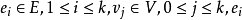 与
与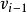 和
和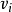 关联,称
关联,称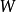 是****图
是****图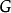 的一条道路,k为路长,
的一条道路,k为路长,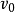 为起点,
为起点,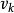 为终点;各边相异的道路称为迹;各顶点相异的道路称为轨道。若
为终点;各边相异的道路称为迹;各顶点相异的道路称为轨道。若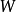 是一轨道,则可记为
是一轨道,则可记为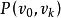 ;起点与终点重合的道路称为回路;起点与终点重合的轨道称为圈,即对轨道
;起点与终点重合的道路称为回路;起点与终点重合的轨道称为圈,即对轨道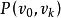 ,当
,当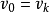 时成为一圈;图中任两顶点之间都存在道路的图,称为连通图。图中含有所有顶点的轨道称为Hamilton轨,闭合的Hamilton轨道称为Hamilton圈;含有Hamilton圈的图称为Hamilton图。称两顶点
时成为一圈;图中任两顶点之间都存在道路的图,称为连通图。图中含有所有顶点的轨道称为Hamilton轨,闭合的Hamilton轨道称为Hamilton圈;含有Hamilton圈的图称为Hamilton图。称两顶点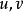 分别为起点和终点的最短轨道之长为顶点
分别为起点和终点的最短轨道之长为顶点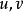 的距离;在完全二分图
的距离;在完全二分图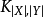 中,
中,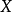 中两顶点之间的距离为偶数,
中两顶点之间的距离为偶数,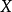 中的顶点与
中的顶点与 中的顶点的距离为奇数。
中的顶点的距离为奇数。
赋权图是指每条边都有一个(或多个)实数对应的图,这个(些)实数称为这条边的权(每条边可以具有多个权)。赋权图在实际问题中非常有用。根据不同的实际情况,权数的含义可以各不相同。例如,可用权数代表两地之间的实际距离或行车时间,也可用权数代表某工序所需的加工时间等。1
相关结论定理1对于图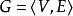 ,有
,有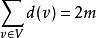 ,其中
,其中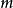 为
为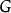 的边数。
的边数。
对于图中的每条边均关联2个顶点,在计算度数时,每条边均提供2度,图有m条边,度数共2m。
在有向图中还有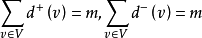 。
。
这个定理称为握手定理,是数学家欧拉于1736年提出,它是图论中的基本定理,由它还可以得到下面的重要推论。2
推论1任一图中,奇数度数顶点的个数为偶数。
**证明:**设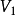 和
和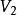 分别为图
分别为图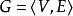 中度数分别为奇数和偶数的顶点集,且
中度数分别为奇数和偶数的顶点集,且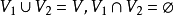 ,
,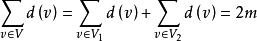 ,则
,则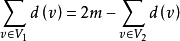 ,由于
,由于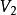 中度数均为偶数,故
中度数均为偶数,故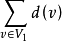 为偶数,只有偶数个奇数的和为偶数,故
为偶数,只有偶数个奇数的和为偶数,故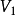 的个数为偶数。
的个数为偶数。
利用推论1可以很方便地判断给定的度数序列能否构成图。如度数序列(3,3,3,1)可以画出图来,而度数序列(3,3,3,2)不可能画出图来。2
定理2**(欧拉公式)**设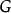 是带
是带 条边,
条边, 个顶点和
个顶点和 个面的平面图,则
个面的平面图,则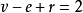 。
。
推论2设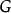 是带
是带 条边和
条边和 个顶点的连通简单平面图,其中
个顶点的连通简单平面图,其中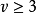 ,则
,则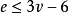 。
。
证明: 由于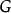 是简单图,因此
是简单图,因此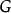 的每个面的度数至少为3。所以图
的每个面的度数至少为3。所以图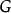 的面的度数之和
的面的度数之和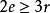 ,其中r为
,其中r为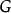 的面数,由欧拉公式得
的面数,由欧拉公式得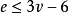 。证毕。
。证毕。
推论3设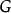 是带
是带 条边和
条边和 个顶点的连通简单平面图,其巾
个顶点的连通简单平面图,其巾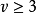 且没有长度为3的圈,则
且没有长度为3的圈,则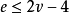 。
。
证明: 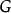 的每个面的度数至少为4。证毕。
的每个面的度数至少为4。证毕。
例1 完全图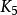 和完全二分图
和完全二分图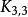 均是非平面图。
均是非平面图。
解: 图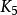 有5个顶点10条边,而3×5-6=9.即10>9,故由推论2知
有5个顶点10条边,而3×5-6=9.即10>9,故由推论2知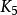 是非平面图;图
是非平面图;图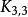 没有长度为3的圈,且有6个顶点9条边,因而9>2×6-4。故由推论3知
没有长度为3的圈,且有6个顶点9条边,因而9>2×6-4。故由推论3知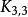 是非平面图。
是非平面图。
推论4设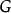 是带
是带 条边,
条边, 个顶点和
个顶点和 个面的平面图,则
个面的平面图,则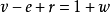 ,其中
,其中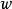 为连通分支数。
为连通分支数。
推论5设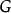 是任意平面图, 则
是任意平面图, 则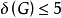 。3
。3


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

