定义
有一类矩阵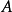 ,如对角矩阵、实对称矩阵(
,如对角矩阵、实对称矩阵(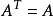 )、实反对称矩阵(
)、实反对称矩阵(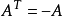 )、厄米特矩阵(
)、厄米特矩阵(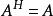 )、反厄米特矩阵(
)、反厄米特矩阵(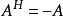 )、正交矩阵(
)、正交矩阵( )以及酉矩阵(
)以及酉矩阵(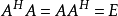 )等,都有一个共同的性质:
)等,都有一个共同的性质: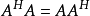 。为了能够用统一的方法研究他们的相似标准型,我们引入正规矩阵的概念。
。为了能够用统一的方法研究他们的相似标准型,我们引入正规矩阵的概念。
设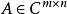 ,且
,且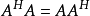 ,则称
,则称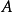 为正规矩阵。
为正规矩阵。
当正规矩阵 的全部特征值为实数时,
的全部特征值为实数时, 是厄米特矩阵;
是厄米特矩阵;
当正规矩阵 的全部特征值为零或虚数时,
的全部特征值为零或虚数时, 是反厄米特矩阵;
是反厄米特矩阵;
当正规矩阵 的全部特征值的模为1时,
的全部特征值的模为1时, 是酉矩阵。
是酉矩阵。
上面提到的几个特殊矩阵都是正规矩阵,但正规矩阵并不限于以上几种。如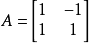 也是正规矩阵,但并不属于上述几种矩阵。1
也是正规矩阵,但并不属于上述几种矩阵。1
性质①矩阵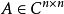 为正规矩阵的充要条件是:存在酉矩阵
为正规矩阵的充要条件是:存在酉矩阵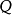 ,使得
,使得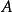 酉相似于对角矩阵,即
酉相似于对角矩阵,即
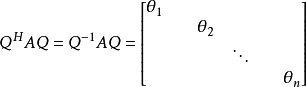 其中
其中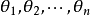 是矩阵
是矩阵 的特征值。
的特征值。
② 为正规矩阵,则与
为正规矩阵,则与 酉相似的矩阵都是正规矩阵;
酉相似的矩阵都是正规矩阵;
③ 为正规矩阵,则
为正规矩阵,则 必有
必有 个线性无关的特征向量;
个线性无关的特征向量;
④ 为正规矩阵,则
为正规矩阵,则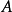 的属于不同特征值的特征子空间是互相正交的。2
的属于不同特征值的特征子空间是互相正交的。2


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

