直言三段论是所有前提都是直言命题的演绎推理。三段论是由包含着一个共同词项的两个直言命题（即：性质判断）推出一个新的直言命题的推理。

定义直言三段论是所有前提都是直言命题的演绎推理。1

例子：

所有动物都会死。

所有人都是动物。

所以，所有人都会死。

前两个命题叫做前提。如果这个三段论是有效的，这两个前提逻辑上蕴含了最后的命题，它叫做结论。结论的真实性建立在前提的真实性和它们之间的联系之上：中项在前提中必须周延（distribute）至少一次，形成在结论中的主词和谓词之间的连接。即使直言三段论是有效的，但如果有前提为假的话结论仍可能是假。

语气和格三段论形式如下：2

大前提：所有M是P

小前提：所有S是M

结论：所有S是P

其中S代表结论的主词（Subject），P代表结论的谓词（Predicate），M代表中词（Middle）。

三段论的命题可分为全称（universal）、特称（particular），及肯定、否定，组合起来有以下四类语气（Mood）：

|| ||

三段论中，结论中的谓词称作大词（P，或称大项），包含大词在内的前提称作大前提；结论中的主词称作小词（S，或称小项），包含小词在内的前提称作小前提；没有出现在结论，却在两个前提重复出现的称作中词（M，或称中项）。大词、中词、小词依不同排列方式，可分成四种格（Figure）：

|| ||

将以上整合在一起，三段论的大前提、小前提、结论分别可为A、E、I、O型命题之一，又可分为4格，故总共有256种三段论（若考虑大前提与小前提对调，便有512种，但逻辑上是相同的）。

三段论依语气与格的分类缩写，例如AAA-1代表“大前提为A型，小前提为A型，结论为A型，第1格”的三段论。

此外，三段论的四种格之间可相互转换：

第1格：不需转换。

第2格：对换大前提的前后两项的位置就变成第1格，对换小前提的前后两项的位置就变成第4格。

第3格：对换大前提的前后两项的位置就变成第4格，对换小前提的前后两项的位置就变成第1格。

第4格：对换大前提的前后两项的位置就变成第3格，对换小前提的前后两项的位置就变成第2格。

E和I命题对换前后两项的位置而保持同原命题等价。A命题不能对换前后两项的位置，但可以在前项确实有元素存在的前提下，转换成与弱于原命题的I命题。O命题不能对换前后两项的位置。

有效性考虑各种直言三段论的有效性将是非常冗长耗时的。幸运的是前人想出了三个可供选择的方法来找出有效性。

还可以通过构造文氏图的方法得到有效形式。因为有三种项，文氏图需要三个交叠的圆圈来表示每一个类。首先，为小项构造一个圆圈。临近小项的圆圈的是同小项有着交叠的大项的圆圈。在这两个圆圈之上是中项的圆圈。它应当在三个位置有着交叠：大项，小项和大项与小项交叠的地方。一个三段论是有效的，其必然条件是通过图解两个前提得出结论的真实性。永不图解结论，因为结论必须从前提推导出来。总是首先图解全称命题。这是通过对一个类在另一个类中没有成员的区域加黑影来实现的。所以在前面例子的AAA-1形式中大前提“所有M是P”中，对M不与P交叠的所有区域加黑影，包括M与S交叠的部分。接着对小前提重复同样的过程。从这两个前提中可推导出在类S中所有成员也是类P的成员。但是，不能推出类P的所有成员都是类S的成员。

作为文氏图方法的另一个例子，考虑形式EIO-1的三段论。它的大前提是“没有M是P”，它的小前提是“有些S是M”，它的结论是“有些S不是P”。这个三段论的大项是P;它的小项是S，它的中项是M。大前提在图中通过对交集M ∩ P加阴影表示。小前提不能通过对任何区域加黑影表示。转而，我们可以在交集S ∩ M的非黑影部分使用x符号来表示“有些S是M”。（注意：黑影区域和存在量化区域是互斥的）。接着因为存在符号位于S内但在P外，所以结论“存在一些S不是P”是正确的。

最后一种方法是记住下面非形式表述的几条规则以避免谬论。尽管文氏图对于诠释目的是好工具，有人更喜欢用这些规则来检验有效性。

基本规则：

结论中周延的词必须在前提中周延（谬误：大词不当、小词不当）

中词必须周延至少一次（谬误：中词不周延）

结论中否定命题的数目必须和前提中否定命题的数目相等：

二前提皆肯定，则结论必须为肯定（谬误：肯定前提推得否定结论）

一前提是否定，则结论必须为否定（谬误：否定前提推得肯定结论）

二前提皆否定，则三段论必无效（谬误：排它前提谬误）

其他检查：

如果语境上不能假设所有提及的集合非空，部分推论将会无效（谬误：存在谬误）

必须包含严格的三个词，不多不少。且须注意所有关键词和结构的语义是否一致（谬误：四词谬误、歧义谬误）

三段论剖析三段论在结构上包括大项、中项和小项。大项是作为结论的谓项的概念，小项是作为结论的主项的概念，中项是在前提中出现两次而在结论中不出现的概念。

三段论的两个前提分别叫做大前提和小前提。其中，包含大项的叫大前提，包含小项的叫小前提。按照通常的习惯，大前提在前面，小前提在后面。但是，排列的顺序不是区分大、小前提的标准。区分大、小前提，只能看它们是包含大项还是包含小项。中项在三段论中十分重要，它起到把大、小前提连接起来，从而推出结论的桥梁和纽带作用。

在三段论中，大项通常用P表示，小项用S表示，中项用M表示。这样，上述推理的一般公式可以表示为：

所有的M都是P。

所有的S都是M。

→ 所有的S都是P。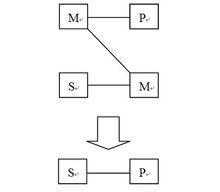

三段论的判定规则

一个三段论是否正确，可以通过下面规则来加以判定。

有且只有三个不同词项

违反这条规则，通常出现的错误成为“四词项”或“四概念”。

中项至少周延一次

中项要起到媒介作用，必须至少有一部分外延既与大项建立关系，又与小项建立关系。如果中项至少周延一次，那么，中项的全部外延就与大项或小项建立了联系，这样就能确保至少有一部分外延同大小项存在关系。违反这条规则，就要犯“中项两次不周延”的逻辑错误。

例如：

坏人都攻击我。

你攻击我。

→ 你是坏人。

上例中的中项“攻击我”，在前提中两次都是肯定命题的谓项，都不周延，犯了“中项两次不周延”的逻辑错误。

前提中不周延的词项结论中也不能周延

这条规则是对大项和小项的外延的规定。三段论是一种必然性的推理，它要求，不能从部分推出全部，不能从不周延的词项过渡到周延的词项，否则推理就不具有必然性了。违反这条规则，就犯了“大项不当周延”或者“小项不当周延”的逻辑错误。

“大项不当周延”是指大项在前提中不周延，而在结论中变得周延了

两个否定前提推不出结论

如果三段论的两个前提都是否定的，那么小项和大项必然都同中项相排斥，这样，中项就无法起到连接大小项的作用，作不出形式有效的推导。

如果前提中有一个否定，那么结论就是否定的

如果前提中有一个是否定的，那么小项和大项之一必然同中项排斥，无论是小项同中项相排斥，还是大项同中项相排斥，在结论中小相同大项必然相排斥，结论必然是否定的。

本词条内容贡献者为:

何星 - 副教授 - 上海交通大学