优势比(odds ratio;OR)是另外一种描述概率的方式。优势比将会告诉我们某种推测的概率比其反向推测的概率大多少。换句话说,优势比是指某种推测为真的概率与某种推测为假的概率的比值。比如下雨的概率为0.25,不下雨的概率为0.75。0.25与0.75的比值可以约分为1比3。因此,我们可以说今天将会下雨的优势比为1**:3(或者今天不会下雨的概率比为3:**1)。
通常情况下,人们习惯于通过与某一主张相反的优势比的方式进行表达,例如,对于“宝马Phar Lap将会在德比赛马中最终胜出”这一主张,人们习惯于使用赔率(即Phar Lap会输的概率比)。然而,科学家们却习惯于使用支持某一主张的优势比。如果我们认为反对两个血样匹配的优势比为1 000 000**:1,那么科学家们习惯于使用支持这一主张的优势比1:1 000 000。可以使用下面的公式,将优势比a:b转换为概率:P=a/(a+b),其中,a是指支持某一主张的概率,b是指反对某一主张的概率。在上述下雨的例子中,支持下雨的优势比为1:**3。因此,a=1,b=3,下雨的概率=1/(1+3)=1/4=0.251。
基本介绍列联表列联表(contingency table)是按两种属性分类的一种统计表,用来说明两种属性之间的关系。一种属性分类为行,另一种属性分类为列。通过列联表可观察两种属性因素之间的相互联系,常用的统计列联表有2×2、2×3、3×3等形式。
列联表是将样本观测数据按两个或更多定性属性分类时所列出的频数表。例如,对随机抽取的1000人按性别(男或女)及色觉(正常或色盲)两个属性分类得到两行两列的列联表 (见表1)。一般地,若总体中的每个个体可按属性A与B分类,A、B分别有r与c个水平,则按样本中属于不同水平组合的频数可以排成r行c列的二维列联表,若考虑的属性多于两个,也可按类似的方法作出多维列联表。
|| ||
优势的概念下面介绍2×2列联表关联性的一种度量-优势比(odds ratio),它是针对属性数据的最重要模型中的参数。
对于成功的概率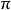 ,成功的优势(odds)定义为
,成功的优势(odds)定义为
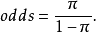 例如,如果
例如,如果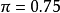 ,则成功的优势为
,则成功的优势为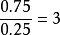 。
。
优势是一个非负实数,当它大于1时成功比失败的概率大。当优势为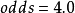 时,成功的可能性是失败的4倍。当成功的概率是0.8时,失败的概率为0.2,则成功的优势为
时,成功的可能性是失败的4倍。当成功的概率是0.8时,失败的概率为0.2,则成功的优势为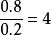 ,于是我们预期每出现1次失败会有4次成功。当
,于是我们预期每出现1次失败会有4次成功。当 ,失败的可能性是成功的4倍,我们预期每出现4次失败会有1次成功。
,失败的可能性是成功的4倍,我们预期每出现4次失败会有1次成功。
成功的概率是优势的函数,
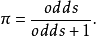 例如,当
例如,当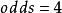 ,那么
,那么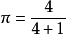 。
。
优势比的定义在2×2表中,第1行成功的优势为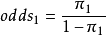 ,第2行成功的优势为
,第2行成功的优势为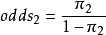 。两行的优势的比值,
。两行的优势的比值,
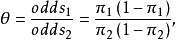 称作优势比,又称比值比或交叉乘积比。相对风险是两个概率的比值,而优势比
称作优势比,又称比值比或交叉乘积比。相对风险是两个概率的比值,而优势比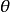 是两个优势的比值2。
是两个优势的比值2。
优势比的性质优势比可以等于任何的非负实数。当X和Y独立,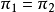 时,
时,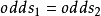 ,从而
,从而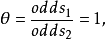 独立值
独立值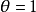 是两组比较的基准。当优势比处于1的两侧,它分别代表了不同类型的关联性。当
是两组比较的基准。当优势比处于1的两侧,它分别代表了不同类型的关联性。当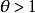 时,第1行中“成功”的优势比第2行大。例如,当
时,第1行中“成功”的优势比第2行大。例如,当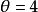 时,第1行中“成功’’的优势是第2行“成功”的优势的4倍。那么,第1行的试验比第2行的试验更容易成功;即
时,第1行中“成功’’的优势是第2行“成功”的优势的4倍。那么,第1行的试验比第2行的试验更容易成功;即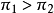 。当
。当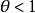 时,第1行试验比第2行的试验更不容易成功:即
时,第1行试验比第2行的试验更不容易成功:即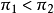 。
。
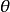 值在给定方向离1.0越远,代表了越强的关联性。优势比等于4时比优势比等于2时有更强的关联性,优势比等于0.25时比优势比等于0.50时具有更强的关联性。
值在给定方向离1.0越远,代表了越强的关联性。优势比等于4时比优势比等于2时有更强的关联性,优势比等于0.25时比优势比等于0.50时具有更强的关联性。
当一个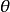 值是另一个值的倒数时,它们具有相同的关联程度,只是方向相反。例如,当
值是另一个值的倒数时,它们具有相同的关联程度,只是方向相反。例如,当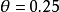 时,第1行成功的优势是第2行成功优势的0.25倍。换句话说,第2行成功的优势是第1行成功的优势的1/0.25=4.0倍。当行或列类别的排列顺序交换以后,新的
时,第1行成功的优势是第2行成功优势的0.25倍。换句话说,第2行成功的优势是第1行成功的优势的1/0.25=4.0倍。当行或列类别的排列顺序交换以后,新的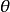 值是原值的倒数。行或列类别的排列顺序通常是任意的,所以不论我们得到的优势比是4.0还是0.25,这仅仅与行和列中各类别是如何排列的有关。
值是原值的倒数。行或列类别的排列顺序通常是任意的,所以不论我们得到的优势比是4.0还是0.25,这仅仅与行和列中各类别是如何排列的有关。
当原表的行和列颠倒后,优势比并不改变,所以表的行可以作为列,列可以作为行,不论我们是把列当作响应变量而把行当作解释变量,还是把列当作解释变量而把行当作响应变量,我们都会得到相同的优势比。所以我们在估计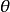 时并不需要去设定某个变量为响应变量,相反的,相对风险需要我们设定响应变量,它的值还依赖于我们是把第一个还是第二个结果类别当作成功。
时并不需要去设定某个变量为响应变量,相反的,相对风险需要我们设定响应变量,它的值还依赖于我们是把第一个还是第二个结果类别当作成功。
当两个变量均是响应变量,优势比能由联合概率决定
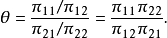 优势比有时也称作交叉积比例,因为它等于对角单元概率的乘积
优势比有时也称作交叉积比例,因为它等于对角单元概率的乘积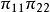 和反对角单元概率的乘积
和反对角单元概率的乘积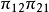 之比。
之比。
样本优势比等于各行样本优势的比,
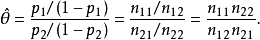 无论是把四个单元当作多项分布还是把两行当作独立二项分布,它都是
无论是把四个单元当作多项分布还是把两行当作独立二项分布,它都是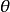 的ML估计2。
的ML估计2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

