基本概念控制系统的数学模型

在控制系统的分析和设计中，首先要建立系统的数学模型。控制系统的数学模型是描述系统内部物理量（或变量）之间的关系的数学表达式。

运动方程在静态条件——变量各阶导数为零——下描述变量之间关系的代数方程叫静态数学模型；

描述变量各阶导数之间的关系的微分方程叫动态数学模型，这些方程就是运动方程。

运动方程的阶次是指运动方程中出现的最高阶导数的阶次，如N阶运动方程就是指方程中出现的最高阶导数是N阶的。

低阶系统低阶系统是指一阶或二阶系统，即以一阶微分方程或二阶微分方程为运动方程的控制系统。在工程实践中，虽然低阶系统的实例较少，但是有些高阶系统的特性可以由低阶系统来近似表征1。

高阶系统高阶系统是指三阶或三阶以上的系统，即以三阶或三阶以上的微分方程作为运动方程的控制系统。在控制系统中，几乎所有系统都是高阶系统。

高阶系统时域分析高阶系统的单位阶跃响应对一般的控制系统，如右图所示，其闭环传递函数为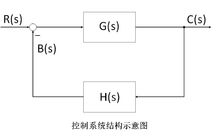

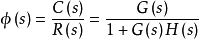
高阶系统可以表示为

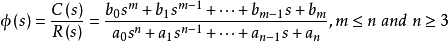
当采用解析法求解高阶系统的单位阶跃响应时，应将上式分子分母多项式分别进行因式分解，再进行反拉氏变换。然后可采用高次代数方程的近似求根法求解。但是高阶系统的阶次越高，这种传统方法的求解就越难。在实际的应用中，一般使用MATLAB 软件对高阶系统进行时域分析。

高阶系统的动态性能在控制系统的实践中，通常要求控制系统既具有较快的响应速度又具有一定的阻尼程度，此外，还要求减少死区、间隙和库伦摩擦等非线性因素对系统性能的影响，因此高阶系统的增益常常调整到使系统具有一对闭环共轭主导极点。这时，可以用二阶系统的动态性能指标来估算高阶系统的动态性能。

高阶系统的简化通常我们研究的控制系统的瞬态响应是较为简单的一阶和二阶系统，但实际系统通常是高阶系统。有时为方便计算，在能够满足一定的精度的情况下，需要把高阶系统的响应简化成低阶系统来近似模拟。

通常高阶系统的简化有两种方法2：

一种是保留原极点的方法 ，另外一种是不保留原主导极点的方法。

保留原主导极点是通过删除传递函数中不太明显的主导极点以达到简化的效果，与其他极点相比，若一个极点具有绝对值很大的负实部，则它对瞬态响应不会产生太明显的影响。这种简化十分简单，但当无法区分出合适的主导极点时，就不能使用这种方法。

不保留极点简化法较为复杂，主要原则是保证降阶后的系统的频率响应尽可能接近原系统的频率相应。