格拉德－沙弗拉诺夫方程为理想等离子体中用角向磁通描述等离子体平衡的方程。该方程最初的形式为二维的，但也可以通过一维格拉德－沙弗拉诺夫方程来描述一维螺旋磁镜位形的等离子体平衡。

详解

其中 为磁导率，为压强，

磁场与电流由下式给定：

的具体形式为：

二维方程

推导（在平板坐标中）

在下文中，假设系统是二维的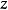 作为不变轴，即 适用于所有数量。然后磁场可以用笛卡尔坐标写成

或者更紧凑

哪里是面内（x和y分量）磁场的矢量势。请注意，基于B的这种形式，我们可以看到A在任何给定的磁场线上都是常数，因为到处都是垂直于B的。1

通过压力和磁力的平衡来描述二维静止的磁结构，即：

其中p是等离子体压力，j是电流。众所周知，p是沿着任何场线的常数，（从那以后）到处都是垂直于B）。另外，二维假设（）表示左手侧的z分量必须为零，因此右手侧磁力的z分量也必须为零。这意味着，即 平行于 .

上一个等式的右侧可以分为两部分：

哪里{\ displaystyle \ perp}下标表示垂直于平面的平面中的分量-轴。该 上述等式中的电流分量可以用一维矢量势写成

飞机场是

并且使用Maxwell-Ampère方程，平面内电流由下式给出

这些结果可以代入表达式中 产量：

以来 和 是一个沿着场线的常量，只有 因此 和 。因此，分解出来和重新排列术语产生Grad-Shafranov方程：

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所