瓦尔德积分是与佩龙积分等价的一种积分。此积分是由瓦尔德(Ward,A.J.)引入的。

简介瓦尔德积分是与佩龙积分等价的一种积分。此积分是由瓦尔德(Ward,A.J.)引入的。

设f(x)是定义在[a,b]上的函数，H(x)与G(x)分别为f( x)的瓦尔德上函数与下函数。若等式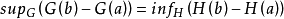成立，则称f(x)在[a,b]上依瓦尔德的意义可积，简称(W)可积，并将上述上、下确界的公共值称为f(x)在[a,b]上的瓦尔德积分。1

相关概念瓦尔德下函数瓦尔德下函数是为定义瓦尔德积分而引进的概念。

设f(x)与G(x)是定义在[a,b]上的函数，若对任意ξ∈[a,b]，存在δ(ξ)>0，使当ξ∈[u,v]⊂(ξ-δ(ξ),ξ+δ(ξ))时有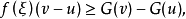则称H(x)为f(x)的瓦尔德下函数。

瓦尔德上函数设f(x)与H(x)是定义在[a,b]上的函数，若对任意ξ∈[a,b]，存在δ(ξ)>0，使当ξ∈[u,v]⊂(ξ-δ(ξ),ξ+δ(ξ))时有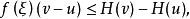则称H(x)为f(x)的瓦尔德上函数。

提出者背景瓦尔德(Wald，Abrahom，1902～1950)美籍罗马尼亚数理统计学家。生于罗马尼亚的克罗日，卒于印度。

先就读于克罗日大学，1927年入维也纳大学学习统计学与经济学，从师门格，1931年获博士学位。

1938年到美国，在哥伦比亚大学工作，1943年任副教授，1944年任教 授，1946年被任命为新建立的数理统计系的执行官员。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学