设Ω是C中的域，如果对任意K⊂Ω，从K⊂⊂Ω能推出Ǩ⊂⊂Ω，就称Ω是全纯凸域。

简介全纯凸包

设Ω是C中的域，K是Ω的一个子集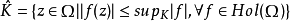，称为K在Ω中的全纯凸包，其中Hol(Ω)表示Ω上全体全纯函数构成的集合。

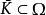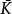如果且是紧的，则称Ω的子集K相对于Ω是紧的，记为K⊂⊂Ω。

全纯凸域

设Ω是C中的域，如果对任意K⊂Ω，从K⊂⊂Ω能推出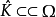，就称Ω是全纯凸域。

全纯域

全纯域是刻画自然边界的域。C中的域Ω称为全纯域，如果不存在比Ω更大的域Ω′(Ω′⊃Ω，Ω′≠Ω)，使得Ω上全部全纯函数都能全纯地开拓到Ω′上去。复平面C上的域都是全纯域，但当n>1时，C中确实存在着非全纯的域。

例如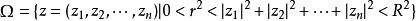：就是非全纯域。这是多复变数函数论和单复变数函数论的一个本质差异之处。1

本词条内容贡献者为:

武伟 - 高级工程师 - 天津直升机有限责任公司