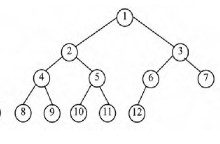
一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。1

定义一棵深度为k且有2k-1个结点的二叉树称为满二叉树。2

根据二叉树的性质2, 满二叉树每一层的结点个数都达到了最大值, 即满二叉树的第i层上有2i-1个结点 (i≥1) 。2

如果对满二叉树的结点进行编号, 约定编号从根结点起, 自上而下, 自左而右。则深度为k的, 有n个结点的二叉树, 当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时, 称之为完全二叉树。2

从满二叉树和完全二叉树的定义可以看出, 满二叉树是完全二叉树的特殊形态, 即如果一棵二叉树是满二叉树, 则它必定是完全二叉树。2

性质1.具有n个结点的完全二叉树的深度为[Log2 n]+1;2

2.如果对一棵有n个结点的完全二叉树的结点按层序编号, 则对任一结点i (1≤i≤n) 有:2

(1) 如果i=1, 则结点i是二叉树的根, 无双亲;如果i>1, 则其双亲parent (i) 是结点[i/2].2

(2) 如果2i>n, 则结点i无左孩子, 否则其左孩子lchild (i) 是结点2i;2

(3) 如果2i+1>n, 则结点i无右孩子, 否则其右孩子rchild (i) 是结点2i+1.2

特点完全二叉树的特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。需要注意的是，满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。1

完全二叉树判定算法思路判断一棵树是否是完全二叉树的思路3

1>如果树为空，则直接返回错
2>如果树不为空：层序遍历二叉树
2.1>如果一个结点左右孩子都不为空，则pop该节点，将其左右孩子入队列；
2.1>如果遇到一个结点，左孩子为空，右孩子不为空，则该树一定不是完全二叉树；
2.2>如果遇到一个结点，左孩子不为空，右孩子为空；或者左右孩子都为空；则该节点之后的队列中的结点都为叶子节点；该树才是完全二叉树，否则就不是完全二叉树；3

代码实现#include #include using namespace std;template struct TreeNode{ T data; TreeNode *left; TreeNode *right; TreeNode(const T &x) : data(x), left(NULL), right(NULL) {}};template bool IsComplete(TreeNode *root){ //1.树为空，返回错误 if (root == NULL) { return false; } //2.树不为空 queue q; q.push(root); while (!q.empty()) { TreeNode *top = q.front(); //2.1如果该节点两个孩子都有，则直接pop if (top->left && top->right) { q.pop(); q.push(top->left); q.push(top->right); } //2.2如果该节点左孩子为空，右孩子不为空，则一定不是完全二叉树 if (top->left == NULL && top->right) { return false; } //2.3如果该节点左孩子不为空，右孩子为空或者该节点为叶子节点，则该节点之后的所有结点都是叶子节点 if ((top->left && top->right == NULL) || (top->left == NULL && top->right == NULL)) { if (NULL != top->left && NULL == top->right) { q.push(top->left); } q.pop(); //则该节点之后的所有结点都是叶子节点 while (!q.empty()) { top = q.front(); if (top->left == NULL && top->right == NULL) { q.pop(); } else { return false; } } return true; } } return true;}//满二叉树void test1(){ // 1 // 2 3 // 4 5 6 7 TreeNode *node1 = new TreeNode(1); TreeNode *node2 = new TreeNode(2); TreeNode *node3 = new TreeNode(3); TreeNode *node4 = new TreeNode(4); TreeNode *node5 = new TreeNode(5); TreeNode *node6 = new TreeNode(6); TreeNode *node7 = new TreeNode(7); node1->left = node2; node1->right = node3; node2->left = node4; node2->right = node5; node3->left = node6; node3->right = node7; cout