参考资料 NASA等

编译 七君

教科书告诉我们，太阳系的八大行星围绕着太阳旋转，太阳是太阳系的中心。画成图大致是这样的——

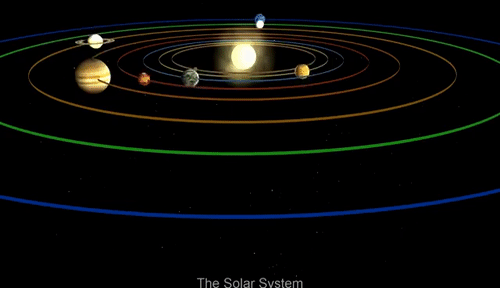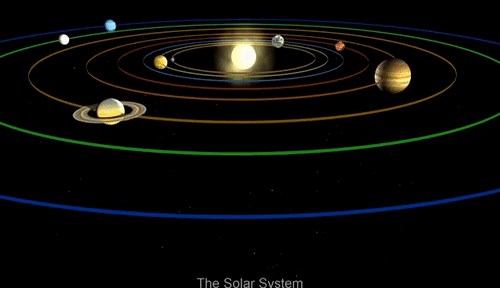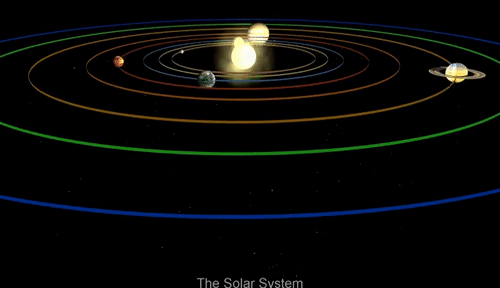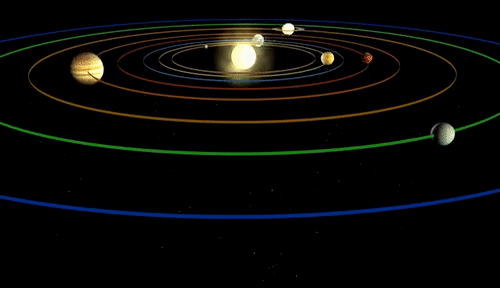
于是乎，当我们想象行星绕着太阳旋转的时候，脑子里总是会出现一个类似于旋转木马的模型，太阳似乎被固定在中心，其他行星绕着太阳的中心旋转。

这种解释方式清晰易懂，适合教学，但实际上它有缺陷。这是因为，太阳系里有一个行星并不围绕着太阳旋转，它实际上在绕着太空中的一个看不见的点旋转。

这个行星就是木星。

木星

@NASA / JPL

是这样的，太阳对行星有引力，行星对太阳也有引力，因此行星绕着太阳旋转时，不动点并不正好是太阳的重心。就比如你和同学互相拉着手转动，不动的那个点既不在你体内，也不在你同学体内，而在你俩之间。

这个不动点，就叫做质心（barycenter），类似于天平的支点。计算质心的位置在哪里是一个典型的二体问题 ，中学生应该算了不少遍了。谁质量更大，质心就更靠近谁；大家质量差不多，质心就居中。

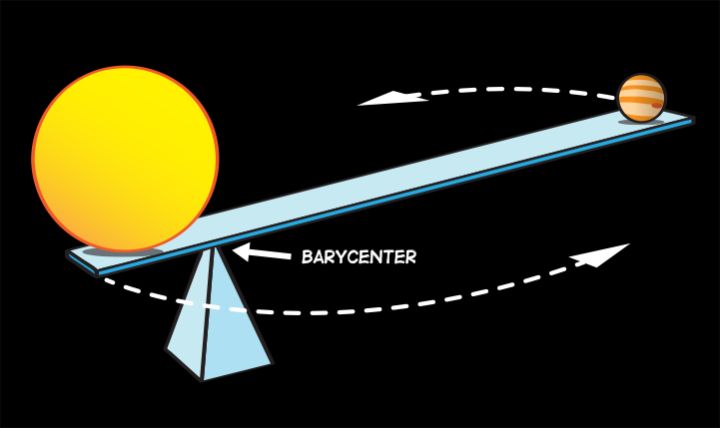
质心

@NASA

就比如在地月系统里，地球和月亮的质心就位于地球半径75%的地方，也就是离地球重心4671千米的地方。

地月系统的质心（黑叉）

@ESA

然而对于太阳系除木星以外的其他行星来说，它们的质量相较于太阳可以忽略不计（如地球的质量只有太阳的0.0003%），因此这个质心总是落在太阳体内，接近太阳的重心。

但是呢，木星的质量是其他所有行星加起来的2倍（木星的质量约是太阳的0.1%），因此木星-太阳的质心距离太阳的重心更遥远，约是太阳半径的1.07倍，大概离太阳表面有4.8万千米，比地球的赤道周长还要长，人类卖出的奶茶首尾连起来不知道能不能够到。

太阳和木星的质心所在位置

@NASA/SDO

换句话说，木星和太阳都围绕着离太阳表面4.8万千米的这个看不见的点旋转。

那么太阳绕着这个质心的转速有多大呢？

因为木星的引力，太阳围绕着质心的旋转速度是13米/秒。作为比较，太阳围绕地球-太阳系统的质心的旋转速度只有9厘米/秒。木星要花11.8年才能绕太阳一周，而太阳绕质心一周的时间也是11.8年。

知道了这个知识点又有什么用？

这非常有用。因为太阳和木星围绕着宇宙中的一个看不见的点旋转，因此在其他地方（其他惯性参考系）看来，太阳会微微抖动。

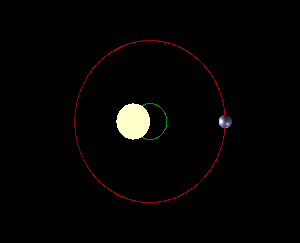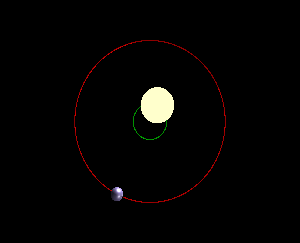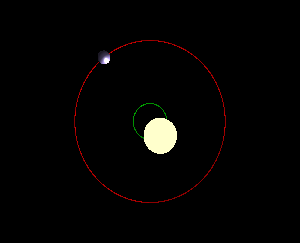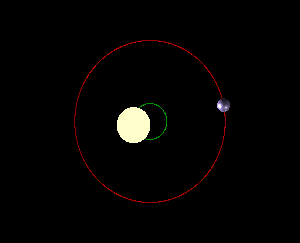
从不同角度观察到的恒星的抖动

@NASA

其实，所有的二体系统都会发生这种抖动，而这种抖动也是天文学家发现绕着恒星旋转的大质量太阳系外行星的一种方法。

从地球上看，如果远处恒星有类似于木星这样的大质量行星，那么它相对于地球的速度就会有周期性的变化。这种变化，会让恒星发出的光一会儿变蓝，一会儿变红。

比如，因为太阳的抖动，太阳光谱——夫琅和费线（Fraunhofer lines）会周期性地一会儿向红光偏移——红移，一会儿向蓝光偏移——蓝移。

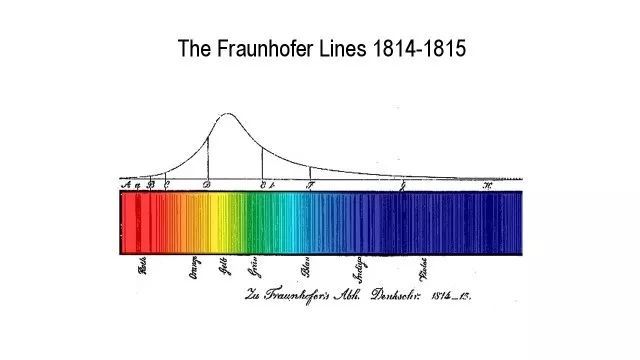
夫琅和费线

其他恒星也是一样，当它们向我们这边抖的时候，它们的夫琅和费线就会蓝移，而当它们抖远的时候，就会红移。这个检测恒星附近行星方法，叫做多普勒抖动（Doppler wobble）。

没有红移或蓝移的光谱（上），红移（中），蓝移（下）

@Caltech

说到转动，还有一个很有意思的现象，这个现象叫做扎尼别科夫效应，是前苏联宇航员弗拉基米尔·扎尼别科夫（Vladimir Dzhanibekov）发现的。

微重力中的扎尼别科夫效应

@NASA

1985年，扎尼别科夫在太空中执行任务时，发现在微重力中旋转的蝶形螺母会周期性地翻转。

微重力中蝶形螺母的扎尼别科夫效应

@engineeringclicks

这个现象把前苏联吓坏了，他们害怕这会引发人类对世界末日的恐慌。你想啊，地球可以看作一个大号的蝶形螺母，而且地球也在围绕着地轴自转。如果扎尼别科夫效应适用于万事万物，那么地球在周期结束后也会180度翻转。到时候地球不就要乱套了？

但是，物理学家们再次拯救了地球。原来，支配扎尼别科夫效应的，是中间轴定理（intermediate axis theorem），而中间轴定理并不适用于地球。

简单来说，如果一个物体（刚体）沿着XYZ轴旋转时，有3个不同的转动惯量（质量乘以质点和转轴的垂直距离的平方），那么就认为它有3个不同的惯量主轴。

T型刚体的3个惯量主轴。红色的那根是中间轴，绕着它旋转产生的转动惯量居中。根据中间轴定理，如果T型刚体绕着它旋转，必定会发生周期性的翻转。

@Randy Dobson

中间轴定理指出，物体只有在沿着能产生最大转动惯量的惯量主轴，或者沿着最小转动惯量的惯量主轴旋转时才比较稳定，沿着中间那个惯量主轴旋转时，必然会发生周期性的翻转。

这就是为什么，你把乒乓球拍绕着下面这个轴丢起来的时候，它肯定会发生翻转。因为这个轴是乒乓球拍的中间轴，绕着它旋转产生的转动惯量既不是最大，也不是最小，非常不稳定。

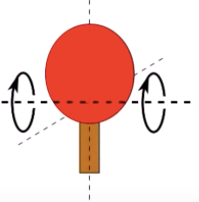
但是这样丢就不会——

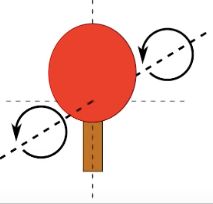
这样丢也不会——

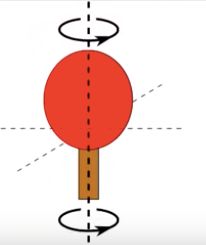
@kettering university

其实，中间轴定理也解释了跳水、体操运动员在旋转和空中转身时手部的动作。

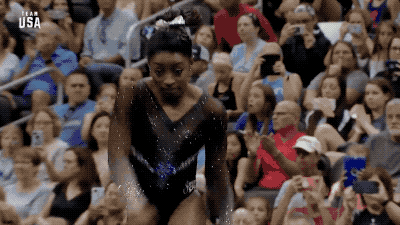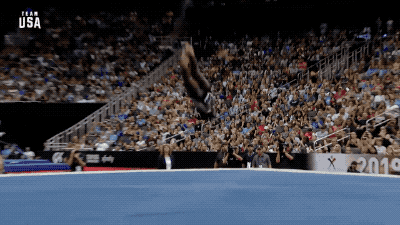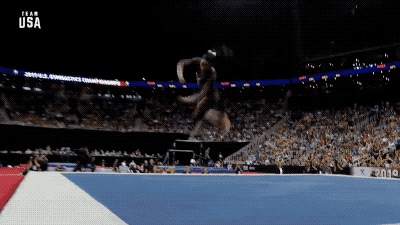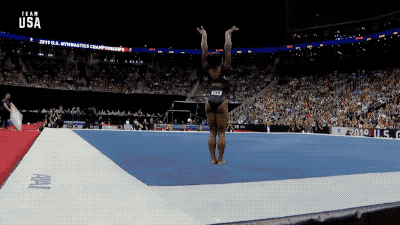
Simone Biles 在2019全美体操竞标赛上的藐视重力的动作

运动员为了做出空翻+转体的动作（wobbling somersault），就要让身体变得不对称，使自己沿着中间轴旋转。所以你可以看到他们会突然一只手向上，一只手向下，摆出超人的姿势。

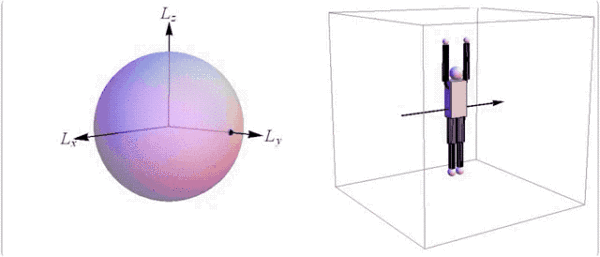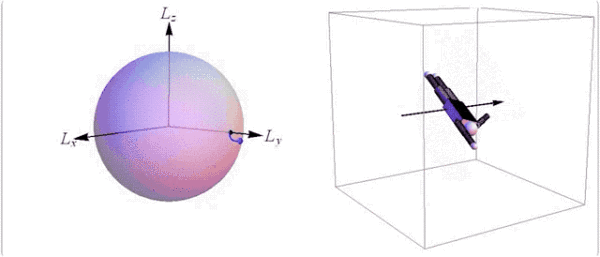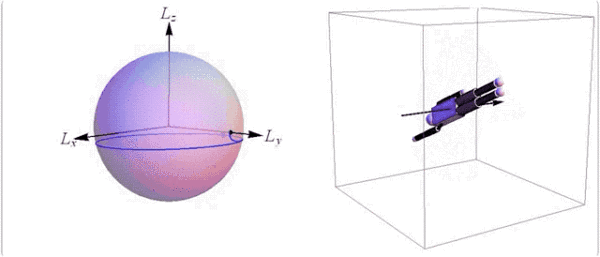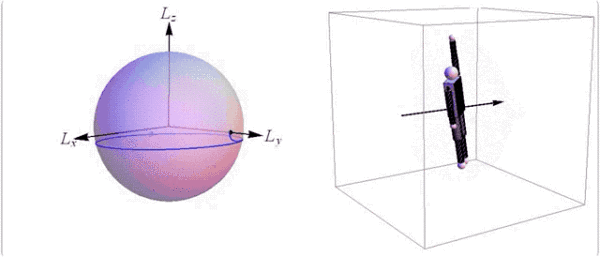
空翻+转体的动作需要在中间轴上旋转，因此身体要不对称。

@Society for Industrial and Applied Mathematics

但是如果不在空中转身（twisting somersault），那么就要保证在最大或最小的惯量主轴上旋转，所以运动员就要让身体保持对称，两个爪子就要对齐。

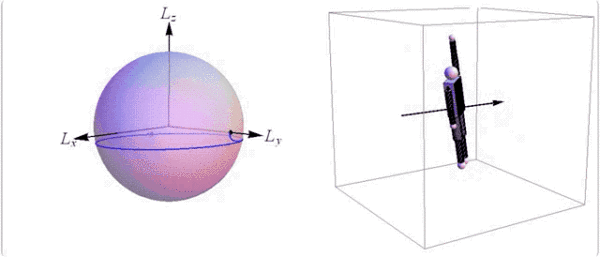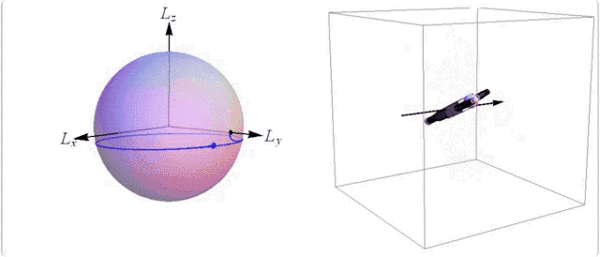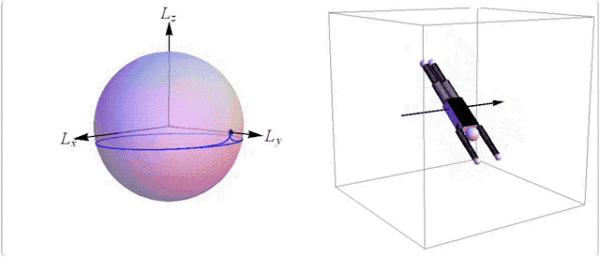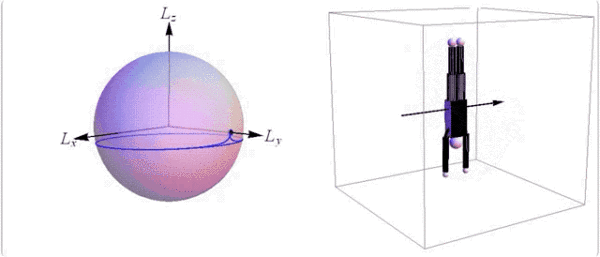
只是做多次空翻旋转，并不转体的话，需要身体在最大或最小惯量主轴上旋转。

@Society for Industrial and Applied Mathematics

话说回来，完美的匀质真空球形鸡不管怎么转，转动惯量都一样大，没有中间轴，无法产生扎尼别科夫效应。

地球也差不多。地球虽然不是一个完美的球体，但赤道附近更加凸起，因此实际上是一个类球面，只有2个不同的惯量主轴，并不存在中间轴，因此不适用于中间轴定理。

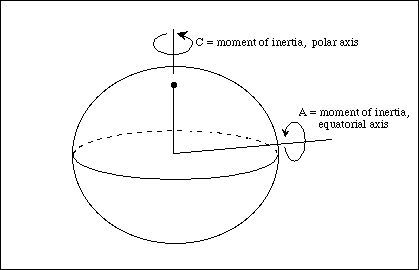
地球只有2个不同的惯量主轴

@columbia university

况且，地球已经沿着产生更大的转动惯量的惯量主轴转动了，因此地球的自转是相对稳定的，不会周期性翻转。害怕地球会突然使出托马斯旋转的街舞招式的同学可以安心洗路了。

对了，猫咪总能四脚着地的定律在太空里却不灵了。战斗种族要是看到喵星人在微重力里的转法，可能会更加怀疑人生吧。大家来吸一下美国联邦航空管理局做的（骗）（经）（费）研究——

来源: 把科学带回家