我想你肯定好奇过，地图上很少有形状规则的国家，那么这些国家的面积是怎么测量出来的呢？特别是在没有计算机技术的年代？

今天就通过一个勺子，来解答你的这个疑问。

关键概念

斧状求积仪

材料和操作

一根木棍

2个不同重量的铁钉

或者一个金属汤勺

制作很简单，只要一根木棍，两端分别钉入2个重量不同的铁钉就可以了，其中一个铁钉要特别重一点，尽量让棍子的重心靠近这个钉子。

做成差不多这样子——

这个数学工具最有意思的地方在于它的使用过程。

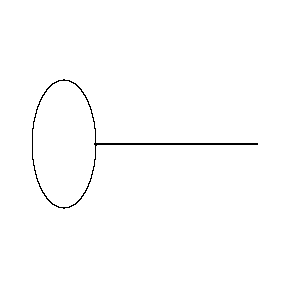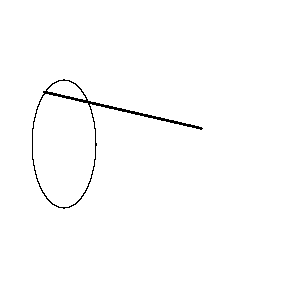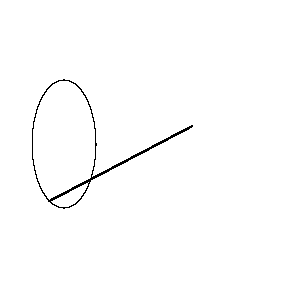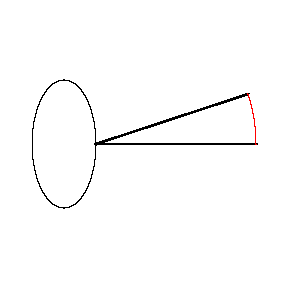
1 把轻的钉子放在图形的边缘上的一点B，重的钉子放在C点。

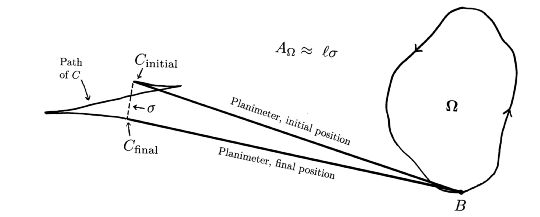
2 B沿着图形移动，最后回到起始点。

3 量一下C的起始和最终位置间的距离 D。量一下棍子本身的长度 L。

图形的面积 ≈ L × D

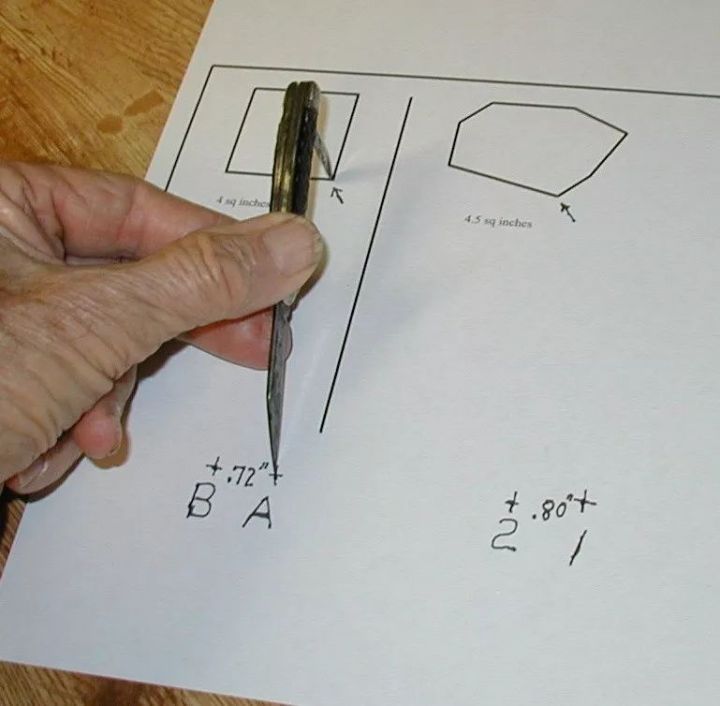
如果你不想做一个斧状求积仪，用一个比较重的金属勺子也可以代替。

看下面这个捷克的网友 Robert Mařík 用同样的测量方法，计算四分之一个圆的面积。

按照他的测量，勺子求积仪测得的面积是0.75，和积分法算得的面积（π/4）的误差约为5%。

你还可以利用各种材料制作斧状求积仪——

瑞士军刀也行——

原理

美索不达米亚的粘土片和埃及的莎草纸证明，人类很早就开始处理面积的问题。

美国第16次人口普查（1940 - 1941年）时，工作人员利用求积仪计算面积。

@The U.S. National Archives

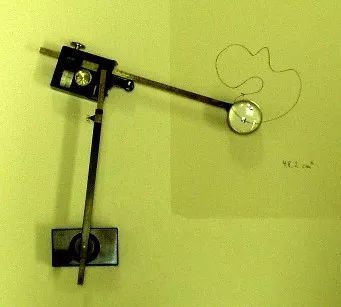
大约在2百年前，人类发明出了能准确计算不规则图形面积的方法，它就是求积仪。求积仪是通过画形状边界线的方式计算面积的数学工具，主要分成两种。

第一种求积仪再沿着边界线滑动的过程中，通过积分来计算面积。这类工具常常用来测量不规则的图形，某个城镇的面积，或者用来测量机器的效率。这类求积仪的计算比较准确。

机械求积仪

@AMS

另一类求积仪虽然也绕着形状边缘画线，但是它对面积仅仅进行了估算。我们制作的斧状求积仪就属于这类。

20世纪初制造的斧状求积仪

@Bob Otnes

斧状求积仪是丹麦数学家，骑兵军官 Holger Prytz 在1875年发明的。1887年，丹麦哥本哈根的 Cornelius Knudsen 公司就开始制造斧状求积仪。

实际上早在1814年，就有人发明了求积仪，后来瑞士数学家 Jakob Amsler-Laffon 在1854年发明的第一类求积仪已经比较接近现代版本了。

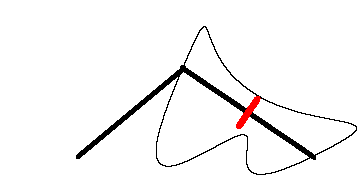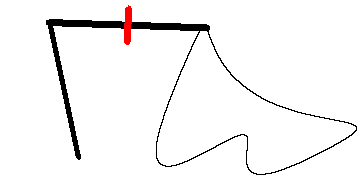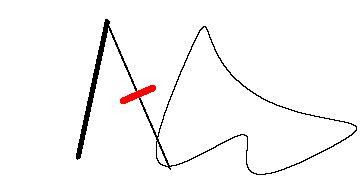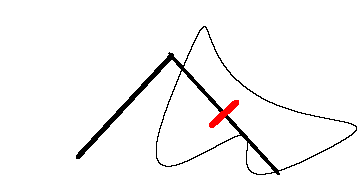
瑞士数学家 Jakob Amsler-Laffon 在1854年发明的求积仪

但是 Prytz 的版本更加经济方便，虽然比 Amsler 的求积仪要不准确一些。

那么，斧状求积仪是怎么算出图形面积的呢？

从数学上来说，斧状求积仪首先利用曳物线（简单来说，一个物体被另一个物体用棍子拖着走时，领先的那一端画出的曲线）对导数进行了近似，并且利用格林公式（Green’s theorem）来求解面积。

面积 ≈ 重的那一头的位移 × 斧状求积仪的长度。

不过，斧状求积仪是近似求解面积，它存在误差。误差和斧状求积仪的长度，以及你画图时的方向（顺时针还是逆时针）有关。我们看这样一个例子。

@wabash.edu

假设斧状求积仪绕着椭圆转了一周。椭圆的长径是4，短径是2，斧状求积仪的长度是5，重的那点移动的距离是红色的这一段圆弧。

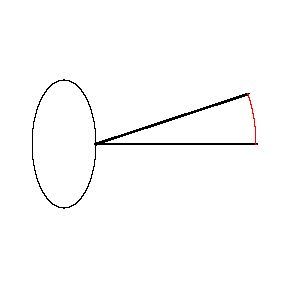
红色圆弧的长度是1.59，因此用斧状求积仪计算得到的椭圆面积是：

1.59 × 5 = 7.94。

直接用椭圆的长径和短径和算得的椭圆面积是2π，也就是6.28。误差达到了26%。

这是为什么呢？

这是因为斧状求积仪相对于要计算的面积太短了。如果用长度为10的斧状求积仪来测量，那么得到的面积是7，误差缩小至11%；如果用长度为20的斧状求积仪测量，那么求得的面积是6.62，误差只有5.3%。

实际上，误差和斧状求积仪的长度约成反比，因此用较大的斧状求积仪测量比较小的面积会更准确。

另外，斧状求积仪旋转的方向对测量结果也有影响。如果长度为5的斧状求积仪从同一个起点，用顺时针绕着同样的椭圆旋转，那么测得的面积是6.77，误差是7.8%，比逆时针时要小。

再来看看斧状求积仪沿着其他规则形状得到的轨迹——

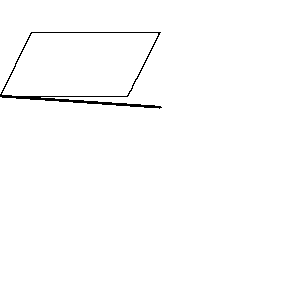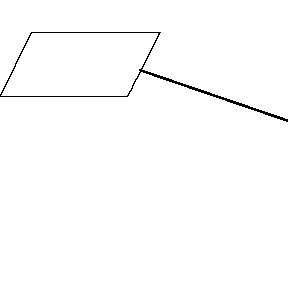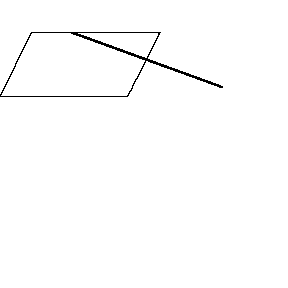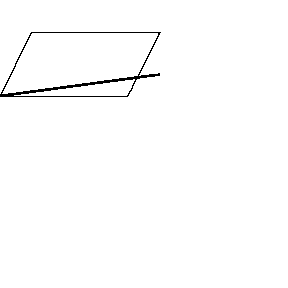
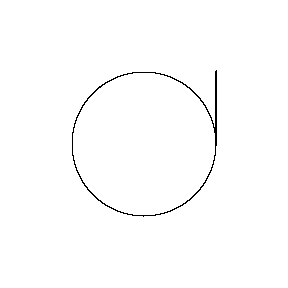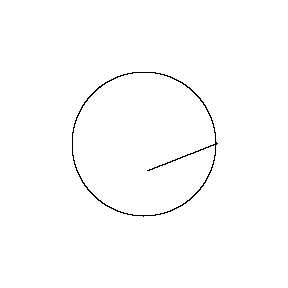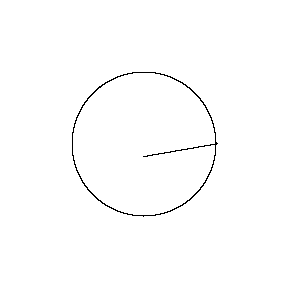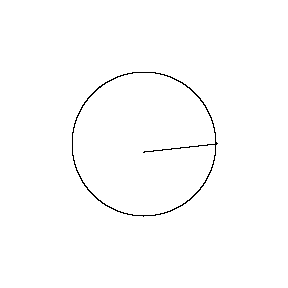
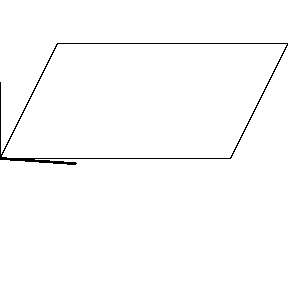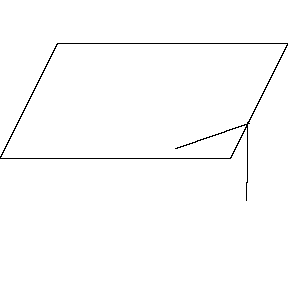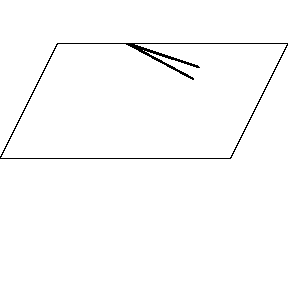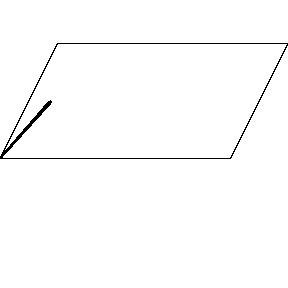
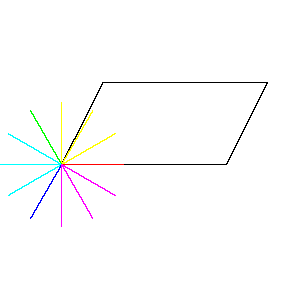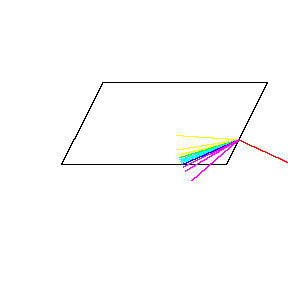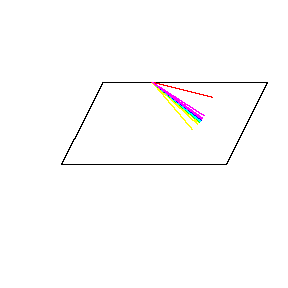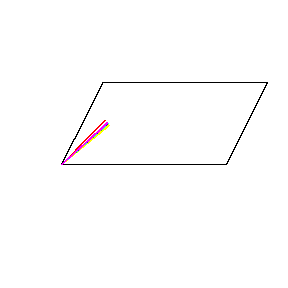
@wabash.edu

测量房间面积的新技能get✔：沿着房间四角爬一圈。

然后用身高乘以 jio 的移动距离。

仅适用于姚明，否则误差太大。

来源: 把科学带回家