编者按

本文是有些哲学意味的科普文章, 后来被收入《交换代数与同调代数》[第二版，李克正著， 科学出版社 (2017)]作为一个附录。

近来出现了不少关于同调代数或范畴论的科普文章, 这有助于公众了解较深刻的数学, 拓宽对于数学的眼界，是很有积极意义的。不过其中有些文章从“数学基础”的眼光讲范畴论, 或者只讲范畴的抽象性, 未免有失偏颇，甚至可能对公众造成误导。

自 19 世纪后期开始, 很多数学家致力于将整个数学建立在集合论的基础之上, 这看上去很美妙, 直到今天也还有人没有放弃这样的努力。但早年的集合概念是“朴素直观”, 却有根本性的漏洞。一般人觉得集合不需要定义直接接受就可以, 但 1902 年罗素给出的“集合论悖论”击溃了这个信念, 使数学家不得不建立集合的公理体系。从哲学上说, 一旦建立起集合的公理体系, 集合论就不可能作为整个数学的基础了。而 1930 年代哥德尔的工作, 更是使数学界认识到，任何建立整个数学的“基础”的企图都是愚蠢的。

不过迄今为止大多数数学学科是建立在集合论基础之上的。比集合更一般的概念是范畴, 但如上所说, 即使范畴论也不能作为整个数学的基础。

范畴是比集合更深的概念, 很多人只看到范畴比集合更抽象, 然而范畴是有结构的, 这种结构的发现源自拓扑学。同调代数中的一些非常抽象的概念, 本是为了解决具体问题的, 而其最主要的价值也正是在于解决具体问题。只看到范畴等概念的抽象性, 类似于“买椟还珠”。

本文力求通过对于分割与粘合, 局部与整体, 连续变形, 自然性等直观在数学中的科学刻画和精准处理, 解释同调代数的产生背景、所解决的具体问题以及其对于数学整体发展所起的作用。

撰文 | 李克正（首都师范大学特聘教授）

引言

20世纪的数学与此前的数学相比，最显著的特点就是整体性。粗糙地说，20世纪前的数学都是“局部的”数学，即使涉及整体的研究对象（如射影空间），也是采用局部的研究方法。研究整体性的根本方法是从拓扑学的建立开始的。而关于整体结构的研究，是在此前关于局部结构的研究已经相当成熟的基础上产生的。

同调代数源自拓扑学。最初同调的定义可以说是组合式的，后来发现同调还可以用其他方式定义，进而在其他领域（如微分几何）用相应领域的方法建立同调，就可以将同调解释为其他领域的不变量。这样同调的方法就逐渐渗透到很多其他学科，包括微分几何、代数、复分析与复几何、李群与李代数、代数数论、代数几何、表示论等，从而产生了很多种同调论，使同调成为数学中的一个重要工具。而这些互不相同的同调论又可以从统一的哲学观点去理解，这就产生了同调代数。在很多发展方向，同调的表现形式、相关结果和应用等离开拓扑学已经如此遥远，以至许多数学研究者在应用同调代数时，竟很难看到自己所采用的方法与拓扑学中的原始思想之间的联系。

本文希望通过对同调代数的起源和发展的观察，特别是从数学角度的理解，说明尽管现代同调代数的应用领域相互间相差甚远，应用形式千变万化，仍可以从其中的基本概念和方法追溯到拓扑学的原始思想。这些思想在今天应该说是数学中的（而不仅是某些数学分支中的）极为重要、基本而深刻的思想。

1

同调的起源

我们先来看看整体性和局部性的区别。

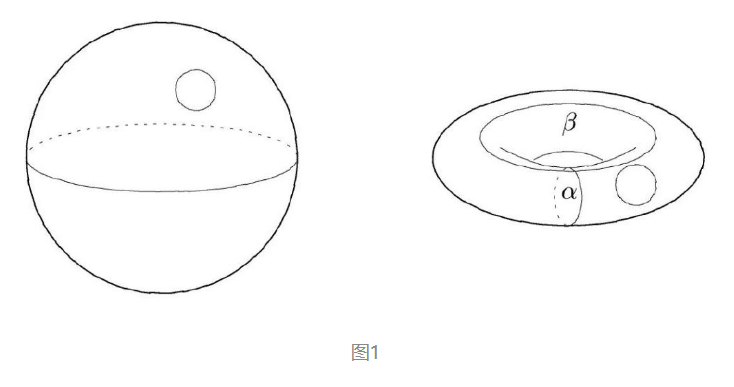
一个典型的例子是曲面的结构。例如球面和环面（图1）的局部结构是一样的，如果在球面或环面上取一小块（如图1中的小圆片），它们的结构都等价于平面上的一小块；但球面和环面的整体结构是截然不同的，如果将球面想象为橡皮，可以随意拉伸变形，甚至还可以剪开翻个身再按原缝粘回去，那么不管怎样做这样的“拓扑变换”，也还是不能把球面变成环面。用拓扑学的术语说，就是球面与环面不“同胚”。由此可见，即使完全了解了局部结构，仍然可能对整体结构毫无所知。

那么，怎样才能说明球面与环面不同胚呢？应该说这是一个困难的问题。如同数学中的很多难题（如罗巴切夫斯基几何不矛盾；五次以上的代数方程没有一般的解法；连续统假设不能证明；方程

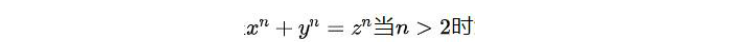
没有全非零的整数解；用圆规和直尺不能三等分任意角，等等）一样，我们不能将球面变为环面，并不是因为我们不够聪明，即使再聪明的人，也还是办不到。要说明这一点，一个基本的想法就是寻找“拓扑不变量”，就是找一种量，它在拓扑变换下不变。对于球面和环面，可以取它们的“亏格”，就是“洞”的个数：环面有1个洞，即亏格为1，而球面的亏格为0，由于亏格是拓扑不变量，这就说明球面与环面不同胚。

用这样的方法就将（拓扑意义下的）曲面转化为若干个三角形相互“粘合”所得的图形，称为“复形”（而三角形则称为单形），这样就将曲面的拓扑结构的研究转化为复形结构的研究。

2

奇异同调和同伦

5

同调代数的产生

同调代数约形成于 1940 年代中期，现在我们所能查到的最早文献是 S. Eilenberg 和 S. MacLane的几篇奠基性的论文（见[3], [4], [5]）。我们来简略地看一下当时和后来建立的基本概念和方法。

总之，同调代数的基本概念如范畴、函子、自然变换、函子的同调、抽象废话等都是很自然地产生的，它们给出了一个很宽广的框架, 可以应用于很多领域，给出不变量、不变性质、等价和约化的方法等（详见第Ⅺ, Ⅻ, XIII章）。还应指出，范畴虽然比集合在逻辑上高一个层次, 仍有更高层次的数学概念，如二范畴（two category）。

同调代数不仅给出强有力的数学工具，给出新的数学课题，而且使数学家从更高的视点观察和理解数学，形成新的哲学理念。

6

同调代数向各数学领域的渗透

同调代数逐渐渗透到数学的很多领域，其中有些领域与拓扑学相距甚远，以至很难看出其与拓扑学中同调的原始思想的联系。我们下面来看几个领域中的初步例子，希望由此说明，虽然有些领域看上去与拓扑学相距遥远，但从其中的同调仍能看到同调论原始思想的内核。

例 1. 纤维丛.

7

Grothendieck建立的一般同调理论

前面我们已经看到，同调的概念和方法可以推广到很一般的范畴和函子。但是所得到的同调可能很抽象，常常需要花很大的工夫才能具体地理解。而且所得到的同调不变量能解决什么问题，能否满足我们的需要，也常常是个问题。

Grothendieck 对于拓扑学和同调代数有非常深刻的理解和洞察。在1960年代，他在代数几何中建立了一套一般的同调论框架，在这个框架中填入一种具体内容就得到一种同调，因此可以根据具体需要填入不同的内容而得到不同的同调理论。

参考文献

[1] P. Deligne, J.S. Milne, A. Ogus and K. Shih: Hodge Cycles, Motives,

and Shimira Varieties, Lecture Notes in Mathematics, LNM, volume 900. Springer-Verlag (1982).

[2] B. Eckmann: Der Cohomologie-Ring einer beliegigen Gruppe. Comment.

Math. Helv. 18 (1945-46), 232-282.

[3] S. Eilenberg & S. MacLane: General theory of natural equivalences.

Trans. AMS 58 (1945), 231-294.

[4] S. Eilenberg & S. MacLane: Relations between homology and homotopy

groups of spaces. Ann. Math. 46 (1945), 480-509.

[5] S. Eilenberg & S. MacLane: Cohomology theory in abstract groups I, II.

Ann. Math. 48 (1947), 51-78, 326-341.

[6] P. Freyd: Abelian Categories. Harper & Row Pub. (1964).

[7] S.I. Gelfand and Yu.I. Manin: Methods of Homological Algebra. 2nd ed.

Springer (2003).

[8] A. Grothendieck and J. Dieudonné: Éléments de Géométrie Algébrique I, Grundlehren 166. Springer-Verlag (1971).

[9] R. Hartshorne: Algebraic Geometry, GTM 52. Springer-Verlag (1977).

中译本: 冯克勤、 刘木兰、 胥鸣伟译, 科学出版社 (1994).

[10] P.J. Hilton and U. Stammbach: A Course in Homological Algebra,

GTM4. Springer-Verlag (1970).

[11] G. Hochschild: Lie algebra kernels and cohomology. Amer. J. Math. 76 (1954), 698-716.

[12] G.M. Kelly and S. McLane: Coherence in Closed Categories. Journal of Pure

and Applied Algebra (1970).

[13] J.-L. Koszul: Homologie et cohomologie des algèbres de Lie. Bull. Soc. Math.

France 78 (1950), 65-127.

[14] 李克正: 《交换代数与同调代数》 第二版, 科学出版社 (2017).

[15] 李克正: 《群概形及其作用论》, 清华出版社 (2018).

[16] S. MacLane: Homology. Springer (1963).

[17] S. MacLane: Categories, GTM 5. Springer (1971).

[18] J.J. Rotman: Notes on Homological Algebra. Van Npstrand Reinhold

Math. Studies 26 (1970).

[19] 周伯壎: 同调代数. 科学出版社 (1988).

出品：科普中国

特 别 提 示

1. 进入『返朴』微信公众号底部菜单“精品专栏“，可查阅不同主题系列科普文章。

2. 『返朴』提供按月检索文章功能。关注公众号，回复四位数组成的年份+月份，如“1903”，可获取2019年3月的文章索引，以此类推。

版权说明：欢迎个人转发，任何形式的媒体或机构未经授权，不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。